
メネラウスの定理は、平面幾何学における三角形と直線に関する重要な定理の一つであり、交点に関する比率を用いた幾何学的関係を記述するものです。この定理は、三角形の外部を通る直線が三角形の各辺またはその延長線と交わる場合、特定の比率が成立するという内容です。特に、三角形の頂点に対する辺の切片の比が関係する点が特徴です。
メネラウスの定理は、チェバの定理と並んで、平面幾何において三角形の内部および外部における交点の性質を明らかにする重要なツールです。これにより、三角形に関連する問題や立体幾何学における立体の断面に関する問題など、さまざまな幾何学的問題を解くための強力な手法を提供します。
歴史的背景
メネラウスの定理は、古代ギリシャの数学者メネラウス(Menelaus of Alexandria, 紀元1世紀頃)の名にちなんでいます。彼は幾何学の分野で著しい貢献をした人物であり、特に球面幾何学における研究で知られています。彼の著書『Sphaerica(球面学)』は、三次元空間における球面の性質とその応用に関するもので、航海術や天文学における問題解決に多大な影響を与えました。
メネラウスは、平面および球面幾何学の研究において、三角形に対する直線の交点が生み出す関係に着目しました。彼が提唱したこの定理は、初期の球面幾何学の研究の一環として、球上の三角形における線の交点に関する法則から発展したものであり、後に平面幾何学における一般的な三角形にも適用されるようになりました。
メネラウスの定理が特に重要視される理由の一つは、それが単なる理論的な数学の道具にとどまらず、実際の物理学や天文学、さらには建築や工学など、さまざまな分野で応用されてきた点にあります。古代から現代に至るまで、この定理は幾何学の基本的な定理の一つとして幅広く認識されており、その影響力は広範囲にわたります。
名前の由来とメネラウスの紹介
メネラウスの定理の名称は、その発見者であるメネラウスに由来します。メネラウスは、古代ギリシャのアレクサンドリア出身の数学者であり、紀元1世紀から2世紀頃に活躍したとされています。彼の業績は、主に球面幾何学と三次元空間における幾何学的問題に関するものですが、彼の名を冠した定理が後世において平面幾何学でも重要な役割を果たしています。
彼の著作『Sphaerica』は、球面上の三角形とその性質を扱い、当時の天文学者や航海士にとって不可欠な知識を提供しました。天体の動きや地球の曲率を考慮した測定を行う上で、球面幾何学の理論は極めて重要であり、メネラウスの業績はその基礎となるものでした。メネラウスの定理も、もともとは球面上での三角形の研究に関連するものでしたが、平面幾何に応用されることでさらに広く知られるようになりました。
このように、メネラウスは古代における数学的・科学的探究の重要な一員であり、その業績は現代においても高く評価されています。彼の名前が付けられた定理は、彼の幾何学的発見の象徴であり、その理論がいかに普遍的で強力であるかを示しています。
メネラウスの定理の定義
メネラウスの定理は、三角形とそれを横切る直線との交点における比の関係を示す幾何学的な定理です。三角形の辺やその延長線が直線と交わるとき、その交点の位置によって辺の切片の比が一定の関係に従うことを示しています。
メネラウスの定理の数式
三角形ABCがあり、直線が辺AB、BC、CAまたはその延長線と交わる点をそれぞれP、Q、Rとします。このとき、メネラウスの定理による比の関係は次の式で表されます:
(AP / PB) × (BQ / QC) × (CR / RA) = 1
この数式は、各辺の切片の比を掛け合わせた結果が常に1になることを示しています。
具体的な定理の説明
メネラウスの定理では、三角形とその辺に対して外部から直線が引かれたときに、それぞれの辺における切片の比率がどのように関連しているかを示します。
- 直線が三角形の辺ABと交わる点をPとする。
- 直線が三角形の辺BCと交わる点をQとする。
- 直線が三角形の辺CAと交わる点をRとする。
この場合、三角形の各辺での切片の比率を求めると、次の関係式が成立します:
(AP / PB) × (BQ / QC) × (CR / RA) = 1
例えば、AP / PBが2:3で、BQ / QCが4:5、CR / RAが6:7であれば、それらの比率を掛け合わせた結果が1でなければなりません。
適用される条件
メネラウスの定理が適用されるためには、次の条件が必要です:
- 三角形ABCとその辺または延長線が交わる直線が存在すること。交点は必ず三角形の各辺またはその延長線上に位置する必要があります。
- 直線は三角形の頂点を通らないこと。この定理では、直線が三角形の頂点そのものを通過する場合には適用されません。
これらの条件が満たされる限り、メネラウスの定理は三角形に対する外部からの直線にも適用されます。
幾何学における定理の重要性
メネラウスの定理は、幾何学における非常に基本的かつ強力な定理です。この定理は、三角形とそれを横切る直線との関係を定量化することで、複雑な幾何学的問題を解決するのに役立ちます。
- 証明や問題解決のツールとして、直線と三角形が交わる問題において、その交点の位置を簡単に把握できます。
- 他の定理との連携: チェバの定理などと組み合わせることで、三角形の内外における直線や交点に関する多くの問題を解決できます。
- 実生活での応用: 測量や天文学の分野でも、三角形と直線の交わりに基づく比の関係を応用して、距離や角度を計算する際に用いられます。
以上の理由から、メネラウスの定理は平面幾何学だけでなく、球面幾何学や立体幾何学においても重要な役割を果たし、数学や物理の広範な分野で応用されています。
メネラウスの定理の証明
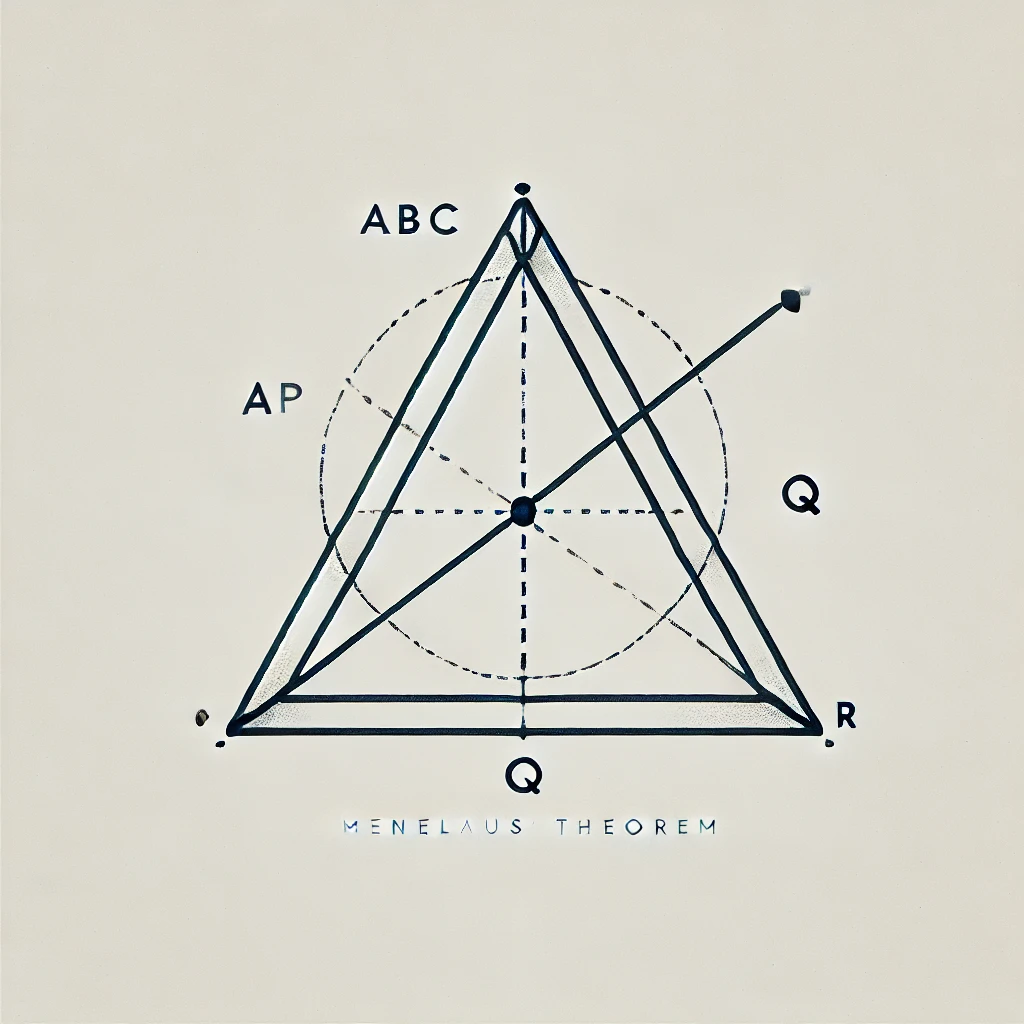
メネラウスの定理は、三角形の各辺またはその延長線上で直線が交わる際の比の関係を表す幾何学的定理です。この定理を用いることで、直線が三角形の辺とどのように交わるかを比で表現し、その比の積が1であることを示すことができます。以下に、メネラウスの定理を証明するステップを示します。
証明の流れ
三角形ABCがあり、直線が辺AB、BC、CAまたはその延長線と交わる点をそれぞれP、Q、Rとします。このとき、メネラウスの定理は次のように表されます:
(AP / PB) × (BQ / QC) × (CR / RA) = 1
ステップ 1: 設定と前提
三角形ABCの各辺AB、BC、CAまたはその延長線に点P、Q、Rが存在し、これらの点は直線と三角形の辺が交わる場所です。ここで、以下のように各辺に対する切片の比を定義します:
- AP
- BQ
- CR
これにより、三角形ABCにおける比の関係を示す準備が整いました。
ステップ 2: 相似三角形を利用した比の導出
次に、相似三角形を利用して、各辺に対する比を導きます。たとえば、三角形APBと三角形CQBが相似であれば、次のように表すことができます:
AP / PB = BQ / QC
他の辺についても同様に相似三角形を使って比を導出します。これにより、各辺の比が同じ構造に従っていることを確認できます。
ステップ 3: 比を掛け合わせる
次に、三角形ABCの各辺の比を掛け合わせます。具体的には、次の式を検証します:
(AP / PB) × (BQ / QC) × (CR / RA)
それぞれの比を代入し、掛け合わせます。
ステップ 4: 結果が1であることを確認
最終的に、比の積が1になることを確認します。これにより、メネラウスの定理が成立することを証明できます。
具体例として、以下の比が与えられている場合を考えます:
- AP= 2:3
- BQ= 4:5
- CR= 6:7
これらの比を掛け合わせると、次のようになります:
(2/3) × (4/5) × (6/7) = 48 / 105
この結果が1に等しくならない場合は、比が正しくないことが分かります。このように、メネラウスの定理を使って比の関係を正確に調整することが必要です。
図を用いた視覚的な説明
- 三角形の構造: 三角形ABCを描き、その辺AB、BC、CAに直線が交わる点P、Q、Rを示します。これにより、各辺の切片に基づく比を視覚的に確認できます。
- 比の計算: 各交点における比を計算し、それらを掛け合わせた結果が1であることを確認します。
代数的アプローチによる証明方法
メネラウスの定理を代数的に証明するためには、相似三角形の性質を使って、各辺に対する比を導き出します。具体的なステップは以下の通りです:
- 相似三角形を使って比を導出: 三角形の頂点と直線の交点によって形成される相似な三角形を見つけ、その対応する辺の比を計算します。これにより、辺の切片に基づく比率が導かれます。
- 比の積の計算: 各辺の切片に基づく比を掛け合わせ、その結果が1であることを確認します。これにより、代数的にメネラウスの定理が成立することが証明されます。
メネラウスの定理は、三角形の辺とそれを交わる直線に対する非常に強力な幾何学的ツールです。三角形の外部または内部を通る直線が三角形の辺に交わる際の比率を明確にし、その積が1になることを示すことで、幾何学的な問題を簡潔に解決できます。この定理は、設計や数学的解析において非常に有用であり、幅広く応用されています。
幾何学問題における実際の応用例
メネラウスの定理は、三角形に対して直線がどのように交わるかを明確に示す幾何学の基本的なツールであり、様々な分野で利用されています。ここでは、幾何学的な問題における具体的な応用例や、現代の数学・物理学での利用、そしてチェバの定理との関係について説明します。
幾何学問題における実際の応用例
メネラウスの定理は、三角形の辺とその延長線上を通る直線が作り出す関係を解明するため、幾何学の様々な問題に応用されています。特に、次のようなケースで役立ちます。
応用例 1: 直線と三角形の交点に関する問題
三角形ABCがあり、任意の直線が三角形の辺AB、BC、CAとそれぞれ異なる点P、Q、Rで交わる場合、メネラウスの定理を用いて各交点の比を求めることができます。
- 三角形ABCを描き、直線が辺AB、BC、CAまたはその延長線と交わる点P、Q、Rを見つけます。
- メネラウスの定理を適用し、次の式を使って比率を計算します:
AP / PB × BQ / QC × CR / RA = 1
これにより、各辺における切片の比を簡単に求めることができ、複雑な幾何学的な配置における交点の比を整理することが可能です。
応用例 2: 三角形内の線分の長さを求める
三角形の内部や外部を通る直線が三角形の辺と交わる場合、その交点の位置や辺の長さを比率に基づいて計算できます。メネラウスの定理を使うことで、三角形の内部を通る直線が頂点を通らない場合でも、その交点の位置を簡単に計算でき、設計や解析に役立ちます。
現代の数学や物理学における利用例
メネラウスの定理は、平面幾何学だけでなく、現代の数学や物理学においても幅広く応用されています。特に、天文学や測量、コンピュータビジョンの分野での活用が見られます。
応用例 1: 球面幾何学における利用
メネラウスの定理は、球面幾何学にも関連する問題から発展したものであり、球面上の三角形の性質を調べるために使われます。これは、地球や天体の表面における大規模な測量や天文学的計算に応用されています。
例えば、航海術や天体の位置を計算する際、球面上の三角形と直線(大円)の交点に関する比率を計算するためにメネラウスの定理が役立ちます。球面三角法の基本ツールとして、特定の位置関係を解く際に利用されます。
応用例 2: コンピュータビジョンや3Dモデリング
コンピュータビジョンでは、3次元空間内の点とカメラ位置を結ぶ幾何学的な関係を扱う際にメネラウスの定理が使われます。3Dモデルの作成時に、複数の視点から見たオブジェクトの投影に関する計算や、カメラのレンズを通して得られる視覚的なデータの解析において、三角形と直線の交点に基づく比率を求める必要があります。
メネラウスの定理と他の定理との関係
メネラウスの定理は、特にチェバの定理と密接な関係があります。この2つの定理は、どちらも三角形と直線に関する性質を記述していますが、適用範囲が異なります。
チェバの定理との比較
チェバの定理は、三角形ABCの内部にある点Pから、頂点A、B、Cに向かって引いた線が、それぞれ三角形の辺BC、CA、ABと交わるとき、次の関係が成り立つことを示します:
AP / PB × BQ / QC × CR / RA = 1
チェバの定理は三角形の内部に適用される一方で、メネラウスの定理は三角形の外部を通る直線にも適用できる点が異なります。
関係性の重要性
これら2つの定理を組み合わせることで、三角形の内外を通る直線に対する幾何学的な比率関係を包括的に理解できるため、さまざまな幾何学的問題に対して強力な解析手段を提供します。特に、設計や建築における構造解析や、複雑な3D空間での視覚情報の処理において非常に役立ちます。
メネラウスの定理は、幾何学における基本的なツールであり、現代の科学や技術分野でも幅広く応用されています。また、チェバの定理との関係を理解することで、三角形に関連する問題をより広範に解決することが可能です。設計、解析、視覚処理など、多くの分野でその重要性が高まっています。
メネラウスの定理を使った練習問題
問題 1:
三角形ABCにおいて、辺AB、BC、CAまたはその延長線上にそれぞれ点P、Q、Rが存在します。直線PQRが三角形ABCの辺またはその延長線を交わっているとき、メネラウスの定理を用いて次の式が成立することを確認してください:
(AP / PB) × (BQ / QC) × (CR / RA) = 1
問題 2:
三角形ABCにおいて、点Pが辺AB上に、点Qが辺BC上に、点Rが辺CA上にあります。次の条件のもとでメネラウスの定理を用いてxの値を求めてください:
- AP = 2、PB = 3
- BQ = 4、QC = 5
- CR = 6、RA = x
問題 3:
三角形ABCの外部を通る直線が、辺AB、BC、CAまたはその延長線と交わる場合を考えます。具体的には、点Pが辺ABの延長線上に、点Qが辺BCの上に、点Rが辺CAの延長線上にあるとき、メネラウスの定理を用いて直線PQRがどのように三角形ABCを横切るかを説明し、辺の切片の比を求めてください。
解答例と解説
解答 1:
メネラウスの定理に基づき、次の式を適用します:
(AP / PB) × (BQ / QC) × (CR / RA) = 1
この式は、三角形の各辺における比を掛け合わせた結果が1になることを示しています。問題文の条件から、この関係が成り立つことを確認できます。
解答 2:
メネラウスの定理を用いてxを求める手順は以下の通りです。
与えられた値を次の式に代入します:
(2 / 3) × (4 / 5) × (6 / x) = 1
まず、左辺の分子と分母を掛け合わせます:
(2 × 4 × 6) / (3 × 5 × x) = 1
48 / (15x) = 1
次に、両辺に15xを掛けて整理します:
48 = 15x
xを求めるために、両辺を15で割ります:
x = 48 / 15 = 3.2
したがって、xの値は 3.2 です。
解答 3:
この問題では、三角形の延長線上に交点が存在する場合を考えます。メネラウスの定理は、三角形の外部を通る直線にも適用できるため、辺の延長線上に交点があっても同様に適用できます。
メネラウスの定理を適用して、次の式を立てます:
(AP / PB) × (BQ / QC) × (CR / RA) = 1
例えば、点Pが辺ABの延長線上にある場合、APとPBの符号が反転するため、比の計算に負の値が含まれることがあります。負の比が発生する場合でも、メネラウスの定理は成立します。
より複雑な応用問題やチャレンジ
応用問題 1:
三角形ABCの外部を通る直線Lが、辺ABの延長線上に点P、辺BCの上に点Q、辺CAの延長線上に点Rを持つとします。各辺の比AP= 2:3、BQ= 4:5、CR= 6:7が与えられています。この直線Lが三角形ABCをどのように横切るかを確認し、メネラウスの定理を用いて比が正しいか確認してください。
応用問題 2:
三次元空間内における三角形の頂点A、B、Cを考えます。この空間内で任意の平面が三角形の辺を交わる点P、Q、Rを持つ場合、メネラウスの定理を拡張して比の計算を行ってください。さらに、直線と三角形が空間内で交わる場合の特殊なケースについて考察し、定理がどのように適用されるかを説明してください。
応用問題 3(チャレンジ):
メネラウスの定理を球面幾何学に応用し、球面上にある三角形と大円が交わる場合の比率を計算してください。地球上の3地点(A、B、C)を結ぶ三角形と、それらの地点を通る飛行ルート(大円)の交点に対して、メネラウスの定理がどのように適用されるかを考え、地球上の測量や航路計算に応用できる方法を示してください。
これらの問題を通して、メネラウスの定理を理解し、さらに高度な幾何学的応用にも取り組むことができます。球面幾何学や三次元空間における問題を考察することで、定理の理解を深めることが可能です。
まとめ
メネラウスの定理は、三角形と直線の交点における比率に関する強力な幾何学的定理です。その数学的意義は、単純な図形構造に対しても、交点の位置や比の関係を精密に求めることができる点にあります。この定理は、三角形内外での直線と辺の関係を扱う際、確かな証拠となるツールとして、幾何学における重要な役割を果たしています。
また、メネラウスの定理は他の定理(特にチェバの定理)と組み合わせて使うことで、三角形の内外を通る直線に関する問題を包括的に解くことが可能です。これは、幾何学的な視点を広げ、より複雑な図形の分析や証明にも役立つ定理です。
幾何学的視点の強化として、メネラウスの定理は、相似形や比の概念をより深く理解するための基礎を提供します。この定理を応用することで、複雑な幾何学問題をシンプルに解く手段を学ぶことができ、数学の基礎力の向上につながります。また、天文学や測量、物理学など、現代の科学技術分野でも応用されており、数学の学問的意義を超えて広範な実用的価値を持っていると言えます。

