数学の世界では、関数の挙動や特性を理解するために多くの定理が存在します。その中でも、ロルの定理は微分積分学において基本的でありながら、非常に重要な役割を果たす定理です。ロルの定理は、関数が特定の条件を満たす場合、その間に極値や傾きがゼロとなる点が存在することを保証します。この定理は、関数の微分可能性や連続性といった基本的な性質を直感的に理解する助けとなり、解析学における他の多くの定理の基礎を築いています。
この記事では、ロルの定理の基本的な定義からその歴史的背景、さらに数学における重要性について詳しく解説します。ロルの定理がどのようにして数学者たちによって証明され、またどのような応用があるのかを学ぶことで、微積分学の基礎をより深く理解することができるでしょう。
ロルの定理とは?
定義: ロルの定理の基本的な説明
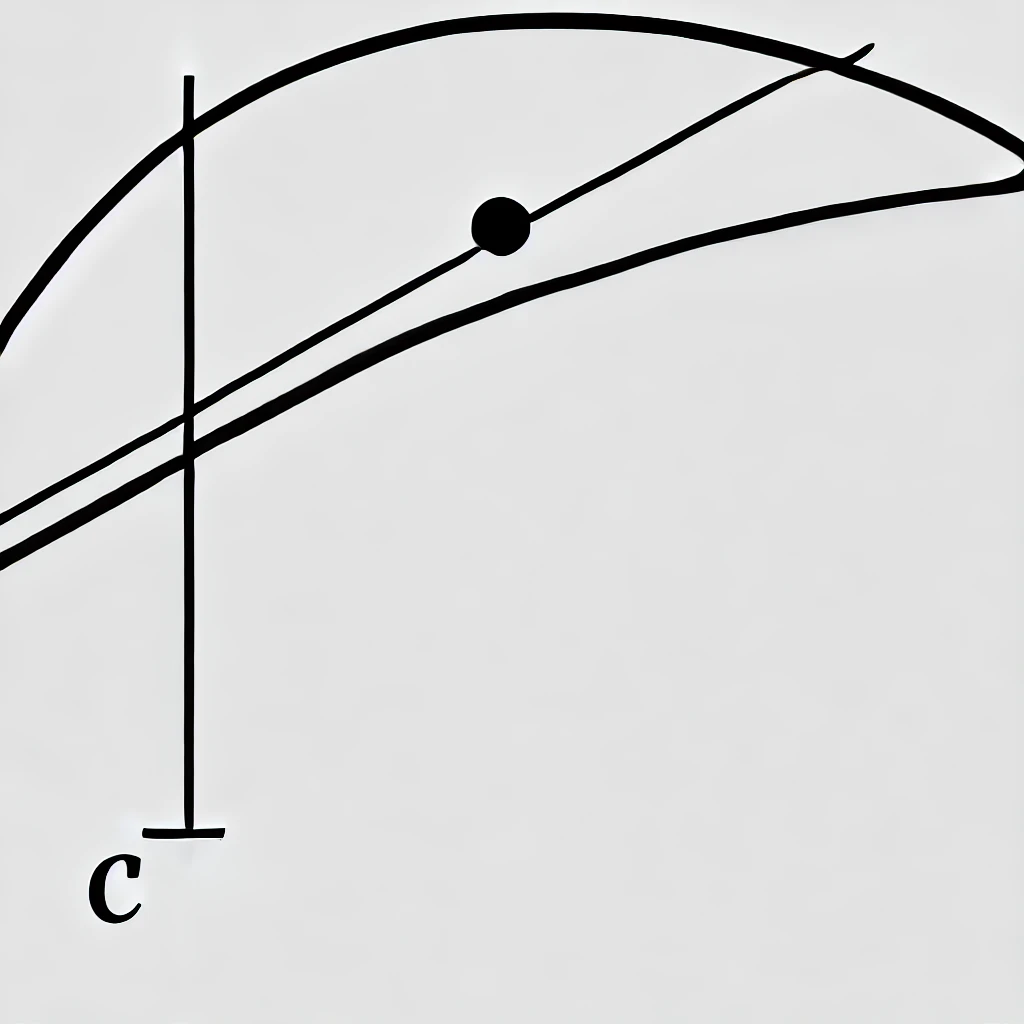
ロルの定理は、解析学における基本的な定理の一つであり、微分可能な関数に関する重要な結果を提供します。この定理は、閉区間上で連続し、開区間で微分可能な関数が、区間の両端で同じ値を取る場合、その間に関数の微分がゼロになる点が少なくとも一つ存在することを示しています。具体的には、次のように定義されます。
関数 f(x) が、閉区間 [a, b] で連続、開区間 (a, b) で微分可能であり、かつ f(a) = f(b) の場合、少なくとも一つの点 c が (a, b) に存在して、次の関係式を満たします:
f'(c) = 0
この定理の本質は、関数が始点と終点で同じ値を持つとき、その途中で必ず水平な接線(傾きがゼロ)を持つ瞬間が存在することです。視覚的には、これはグラフが山や谷を描く形で極値を持つことを意味します。
歴史的背景: ロルの定理が数学において重要な位置を占める理由
ロルの定理の名は、17世紀のフランスの数学者、ミシェル・ロル(Michel Rolle)に由来しています。彼は1691年にこの定理を発表しましたが、その内容は既に知られていたものの、彼が形式的に証明したことから「ロルの定理」として知られるようになりました。
ロルの定理は、解析学において平均値の定理の基礎的なバージョンとして位置づけられます。実際、平均値の定理はロルの定理を拡張した形で成り立っており、そのためこの定理は多くの微分積分学の定理の土台をなすものとして重要です。
また、ロルの定理は極値や停留点(関数の傾きがゼロになる点)の存在を保証するため、極限、微分、最適化の分野で応用されています。この定理は、関数の特定の性質を厳密に理解するために不可欠であり、様々な数学的証明や解析において基本的なツールとなっています。
数学史においても、ロルの定理は17世紀の微積分の発展に寄与し、後に平均値の定理やテイラー展開といったより高度な結果の基礎を築く上で極めて重要な役割を果たしました。このように、ロルの定理は現代数学においても、その理論的意義と実用性の両方から、強力な定理として高く評価されています。
ロルの定理の前提条件

ロルの定理が適用されるためには、関数がいくつかの特定の条件を満たしている必要があります。これらの前提条件が守られて初めて、定理が正しく成り立ち、その結果が保証されます。ここでは、ロルの定理の前提条件である微分可能性と連続性、そして定理が適用される条件について詳しく説明します。
微分可能性と連続性の必要性
ロルの定理が成り立つためには、関数は次の2つの条件を満たす必要があります。
1. 連続性
関数 f(x) は、閉区間 [a, b] で連続でなければなりません。これは、関数が区間内のどの点においても突然のジャンプや不連続な変化がないことを意味します。連続性が必要な理由は、関数が滑らかに変化することで、その区間内のどこかに微分がゼロになる点が必ず存在することを保証するためです。もし関数が不連続であれば、グラフ上に途切れた部分が現れ、そのような点での接線(傾き)を求めることが不可能になります。
2. 微分可能性
関数は、開区間 (a, b) において微分可能でなければなりません。これは、区間内のどの点においても関数の瞬間的な変化率、つまり接線の傾きを計算できることを意味します。微分可能性が重要な理由は、ロルの定理が「関数のどこかで接線が水平になる点(微分がゼロになる点)が存在する」ということを示しているためです。もし微分可能性がなければ、その点での傾きを求めることができず、定理の適用が不可能になります。
さらに、微分可能性を保証するためには、連続であることが前提となります。関数が連続でない場合、微分可能であることは期待できません。
定理が適用される条件
ロルの定理が適用されるためには、上記の微分可能性と連続性に加えて、次の条件が満たされる必要があります。
始点と終点での値が等しいこと
つまり、関数の両端において f(a) = f(b) であることが必要です。この条件は、関数が閉区間の端で同じ高さ(値)を持っていることを示しています。この場合、グラフは閉区間内で「上昇して下がる」か「下降して上がる」という形になり、途中で少なくとも一度、傾きがゼロになる点が現れることが保証されます。
例えば、ある曲線が区間の始点と終点で同じ値を取る場合、その区間内で必ず一度は上昇・下降やその逆の動きが生じます。このとき、どこかで「平らな部分」、つまり微分がゼロとなる点が存在するはずです。この点こそがロルの定理が保証するものであり、関数の性質を理解する上で重要な役割を果たします。
このように、関数の連続性と微分可能性、そして始点と終点での値が等しいという条件は、ロルの定理が正しく適用されるために不可欠です。これらの条件が満たされることで、関数がどこかで接線が水平になる点を持つことが保証され、関数の解析において重要な結論を導き出すことが可能となります。
ロルの定理の応用例
ロルの定理は、解析学における基礎的なツールであり、特に極値の存在を証明したり、他の重要な定理の基礎として使用されることが多いです。また、数学的な理論を現実世界の問題に適用するための道具としても役立っています。ここでは、解析学における応用例と実生活での応用例を紹介します。
1. 解析学における応用
a. 極値の存在証明
ロルの定理は、極値の存在を証明する際に頻繁に用いられます。極値とは、関数が区間内で最大または最小の値を取る点のことです。ある関数が区間の両端で同じ値を持つ場合、その区間内に極値が必ず存在することをロルの定理は保証します。
例えば、連続かつ微分可能な関数が閉区間 [a, b] で定義されており、両端で同じ値 f(a) = f(b) を持つ場合、その区間内に少なくとも一つの点 c が存在し、その点で f'(c) = 0 となることが示されます。これにより、その区間内に極大または極小値が存在することが証明されます。
b. 平均値の定理の基礎
ロルの定理は、平均値の定理の基礎として使用されます。平均値の定理はロルの定理を一般化したもので、関数がある区間内で連続かつ微分可能であれば、その区間内に「関数の瞬間的な変化率が、区間全体の平均変化率と等しくなる点」が存在することを示します。
ロルの定理では、両端が同じ値を持つ場合に適用されますが、平均値の定理は両端の値が異なる場合にも適用され、より一般的な状況に対応しています。
c. 他の定理の証明における使用
ロルの定理は、解析学の他の重要な定理の証明にも頻繁に使われます。例えば、テイラーの定理やラグランジュの平均値の定理などは、ロルの定理に基づいて証明される部分があり、これらの定理の重要なステップとして機能しています。このように、ロルの定理は、他の高度な解析学の結果を導くための基礎となっています。
2. 実生活での応用
ロルの定理は、現実世界の問題に直接適用されることは少ないですが、数学的なモデルや分析を行う際に間接的に活用されています。具体的な応用例をいくつか紹介します。
a. 機械工学や物理学における応用
機械工学や物理学では、物体の運動や力学的変化を解析する際に、ロルの定理が役立ちます。例えば、物体が始点と終点で同じ速度を持つ場合、その間に少なくとも一度は速度がゼロになる瞬間が存在することをロルの定理は保証します。これは、物体が一度静止することを意味し、運動の解析や機械の制御において重要な情報を提供します。
b. 最適化問題における応用
経済学や工学の分野では、最適化問題においてロルの定理が役立ちます。たとえば、コスト関数が連続かつ微分可能である場合、その区間内でコストが最小となる点が存在することをロルの定理が保証します。これにより、特定の範囲内で極値を見つけることができます。
c. 金融市場における応用
金融市場では、株価や資産価格の変動を分析する際に、関数の極値や停留点を調べることが重要です。ロルの定理は、価格が上昇と下降を繰り返す期間内に、価格変動の傾きがゼロになる点が存在することを保証します。これにより、価格の転換点やトレンドの変化を予測する際に役立ちます。
ロルの定理は、解析学の基礎として重要な役割を果たすだけでなく、実際の問題解決にも応用されることがあります。特に物理学、最適化、経済学など、関数の挙動を分析する場面で間接的に利用され、現実世界の問題を数学的に理解するためのツールとして広く活用されています。
ロルの定理と平均値の定理との違い

ロルの定理は、平均値の定理を理解するための基礎となっています。ロルの定理では、関数 f(x) が閉区間 [a, b] で連続し、開区間 (a, b) で微分可能で、両端点で同じ値 f(a) = f(b) を取る場合、その区間のどこかに f'(c) = 0 となる点が存在することを示しています。これを拡張して、両端の値が異なる場合を考えるのが平均値の定理です。
平均値の定理は次のように述べられます:
関数 f(x) が閉区間 [a, b] で連続し、開区間 (a, b) で微分可能であるならば、少なくとも一つの点 c が (a, b) に存在し、次の式を満たします:
f'(c) = (f(b) - f(a)) / (b - a)
この式は、区間 [a, b] における関数の平均変化率と、ある点における接線の傾き(瞬間的な変化率)が一致することを示しています。ロルの定理が「接線が水平になる点が存在する」ことを示すのに対し、平均値の定理は「区間全体の平均変化率と一致する瞬間の接線が存在する」ことを示しています。
ロルの定理は、特別な場合(つまり f(a) = f(b) の場合)の平均値の定理とみなすことができ、これが両者の直接的な関係です。
両者の違いと類似点
類似点:
- 両方の定理は、関数が連続性と微分可能性という同様の前提条件を持つことを要求します。
- 両者とも、関数の中間にある特定の点 c に関して、接線の傾きや瞬間的な変化率が特定の条件を満たすことを示しています。
違い:
- ロルの定理では、区間 [a, b] の両端で同じ値を持つ関数に限定され、必ず水平な接線を持つ点が存在することを示しています。一方で、平均値の定理は、両端の値が異なる場合にも適用され、関数の平均変化率と一致する接線が存在することを保証します。
- ロルの定理が「特別な場合の結果」であるのに対し、平均値の定理はより一般的で幅広い状況に対応します。
まとめ
ロルの定理の重要性の総括
ロルの定理は、微分積分学において基本的かつ重要な定理の一つです。この定理は、連続性と微分可能性の概念に基づいて、関数の挙動を深く理解するための道具となります。特に、極値の存在を証明するために不可欠であり、関数の変化を解析するための基礎を築いています。また、ロルの定理は平均値の定理の基礎となり、微分積分学における他の多くの定理の土台となる重要な位置を占めています。
さらなる学びへの道筋
ロルの定理を学ぶことは、数学のさらなる発展的な理論を理解する上での重要なステップです。この定理を基にして、平均値の定理、テイラーの定理、および微分の応用など、より高度な解析学の定理や技法へとつながります。これらを深く理解することで、関数の性質や変化を詳細に解析し、さまざまな数学的および現実の問題を解決するための強力なツールを手にすることができるでしょう。

