パスカルの定理は、フランスの数学者ブレーズ・パスカルによって17世紀に提唱された射影幾何学の基本定理の一つです。この定理は、円に内接する六角形の対辺の交点に関する幾何学的関係を述べており、初等幾何学においても重要な役割を果たしています。具体的には、円に内接する任意の六角形の対辺を延長すると、それらが3箇所で交わり、その交点は常に一直線上にあるという内容です。この一直線上に並ぶ性質は、パスカル線と呼ばれています。
この定理の重要性は、初等幾何学だけでなく、射影幾何学の基礎を築いた点にあります。パスカルの定理は、射影幾何学におけるデザルグの定理と並ぶ重要な定理であり、特に直線と円の関係を記述する上で、円錐曲線や他の二次曲線にも拡張可能な一般的な性質を示しています。パスカル自身はこの定理を16歳という若さで発表しており、彼の天才的な数学的直感を象徴する結果とされています。
もう少し詳しく定理の内容を見ていくと、六角形の頂点をA, B, C, D, E, Fとし、ABとDE、BCとEF、CDとFAという対辺を考えます。これらの対辺をそれぞれ延長したとき、その交点がP, Q, Rと呼ばれる点で一直線上に並びます。この「一直線上にある」という条件は、射影幾何学における基本的な性質であり、古典的なユークリッド幾何学では発見できない、新しい次元の見方を提供しています。
パスカルの定理はまた、メネラウスの定理やセバスチャン・ブリアンションの双対定理とも関連しており、これらと併せて研究することで、二次曲線に対する深い理解を得ることができます。さらに、円の特別な場合だけでなく、他の円錐曲線(楕円、放物線、双曲線)に対しても同様に成り立つことから、定理の応用範囲は広範です。
現代において、パスカルの定理は射影幾何学の教育や研究の中で不可欠なものとなっており、幾何学的構造や座標幾何の問題を解く際の基本ツールとしても使われています。この定理を通じて、幾何学的図形の関係や性質をより深く理解するための道筋が開かれているのです。
歴史的背景: パスカルの定理とその影響
1. パスカルの生涯と業績
ブレーズ・パスカル(1623-1662)は、フランスの数学者、物理学者、哲学者として知られ、その幅広い業績が現代にも影響を与えています。彼は幼少期から数学的な才能を発揮し、16歳の時にはすでに著名な数学者であったデカルトやフェルマーと議論を交わすほどの名声を得ていました。彼の研究は数学に留まらず、流体力学や気圧の研究、確率論、さらには哲学や宗教的著作にまで及び、幅広い分野で功績を残しています。
パスカルはまた、確率論の基礎を築いたことで知られ、現代の統計学や経済学の発展にも大きな影響を与えました。特に彼の友人であり、フェルマーとの書簡を通じて発展した確率論の研究は、ギャンブル問題などから発想を得たものでしたが、後に保険やリスク管理など、様々な分野に応用されることとなりました。
2. 幾何学への貢献
パスカルは特に幾何学においても重要な業績を残しており、その一つが16歳の時に発表した「パスカルの定理」です。彼はこの定理を通じて、円に内接する六角形に対する新しい幾何学的な性質を発見しましたが、それ以上に、この発見が射影幾何学という分野の基盤を築く重要なものであった点が注目されています。
射影幾何学は、伝統的なユークリッド幾何学の制約を超えた視点を提供し、直線や点、円錐曲線などの間に成り立つ関係性をより広く理解するためのツールです。パスカルは、円錐曲線上にある六つの点から六角形を構成し、その対辺の延長が一直線上で交わるという、ユークリッド幾何学では見過ごされていた深い性質を見出しました。この業績により、後の数学者たちは幾何学の新しい方向性を探求するようになりました。
3. パスカルの定理の発見と発表の経緯
パスカルの定理は、彼がまだ16歳という若年で発表されたもので、当時の数学者たちを驚嘆させました。この定理は「パスカルのミステリックヘキサグラム」として最初に発表され、彼の天才的な数学的直感が反映された成果とされます。
この定理は、パスカルが射影幾何学の可能性を初めて認識した瞬間でもあり、後の数学において重要な一歩となりました。パスカルはこの定理を数学界に公表し、後の数学者たちによって幾何学の他の問題に応用されるようになりました。彼の若さにも関わらず、その発見の深遠さは、同時代の数学者たちの尊敬を集めました。
4. 当時の数学界における影響
パスカルの定理は、当時の数学界に大きな影響を与えました。この発見は、従来のユークリッド幾何学の枠組みを超える射影幾何学の可能性を示し、数学の進展において重要なステップとなりました。特に、デザルグの定理やメネラウスの定理などと並んで、幾何学における深い対称性や位置関係の理解を助け、幾何学の基礎理論に対する認識を大きく変えるものとなりました。
パスカルの定理はその後、他の二次曲線(円錐曲線)に対しても一般化され、射影幾何学の発展に寄与しました。この定理が示した新たな視点は、19世紀に至るまで射影幾何学の理論構築において非常に重要な役割を果たし、数学の他の分野、特に解析幾何学や代数幾何学にも影響を与えました。
このようにして、パスカルの定理は単なる個別の発見に留まらず、数学の理論的発展において革新をもたらす礎となりました。
パスカルの定理の定義

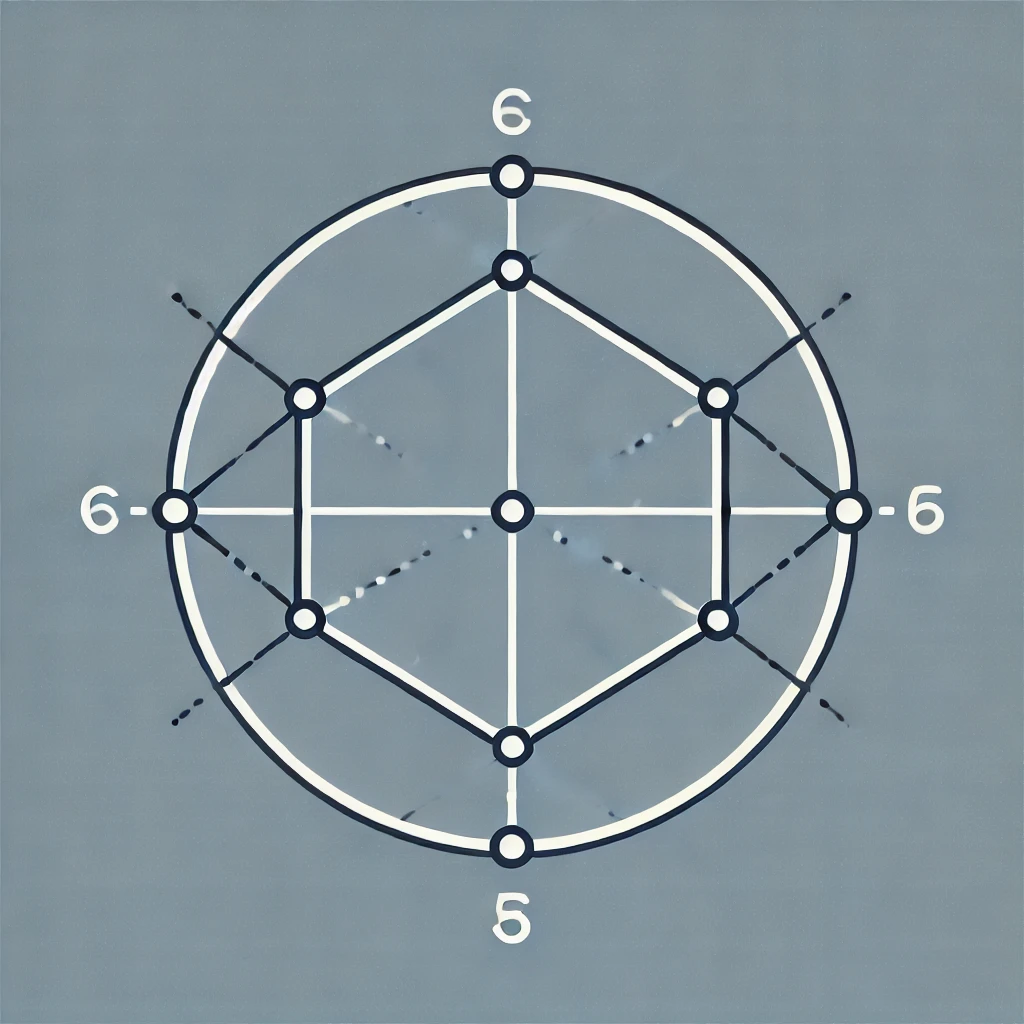
パスカルの定理は、円に内接する六角形に関する幾何学的性質を述べたもので、円に内接する任意の六角形において、その対辺を延長すると、それらの延長線が3点で交わり、その交点が一直線上に並ぶという定理です。この一直線上に並ぶ交点を「パスカル線」と呼びます。
定理の具体的な内容
1. 円に内接する六角形
任意の円に内接する六角形 ABCDEF を考えます。この六角形は、円周上の6つの頂点 A, B, C, D, E, F を持ち、それぞれ隣り合った辺を持つ閉じた図形です。
2. 対辺の延長
六角形の3組の対辺を考えます。対辺とは、隣り合わない辺の組合せで、以下のようになります。
- 辺 AB と DE
- 辺 BC と EF
- 辺 CD と FA
これらの辺を直線として延長します。
3. 交点の発生
延長された対辺がそれぞれ交わる点を次のように名付けます。
- AB と DE の交点を P
- BC と EF の交点を Q
- CD と FA の交点を R
4. 交点が一直線上に並ぶ
パスカルの定理によれば、これら3つの交点 P, Q, R は必ず一直線上に並びます。この直線を「パスカル線」と呼びます。
射影幾何学的視点
パスカルの定理は、円に限らず、楕円や双曲線などの他の円錐曲線にも適用可能です。つまり、円の代わりに二次曲線に内接する六角形でも同じ性質が成り立ちます。この性質は、射影幾何学における基本的な構造を示しており、直線や点の射影的関係性に基づいています。
この定理は、射影幾何学の基礎を学ぶ上で非常に重要な役割を果たし、幾何学的な対称性や構造を理解するための鍵となります。
パスカルの定理の証明
初等幾何学的証明
1. 六角形の設定
円に内接する任意の六角形 ABCDEF を考えます。この六角形の頂点はすべて円周上にあり、順番に並んでいます。
2. 対辺の延長と交点の設定
定理の条件に従い、以下の対辺を延長し、それぞれの交点を求めます。
- 辺 AB と DE の交点を P
- 辺 BC と EF の交点を Q
- 辺 CD と FA の交点を R
3. 角度の等式の利用
三角形の性質を用いて、特定の角度が等しいことを示します。例えば、三角形 ABP と DEP において、対応する角度が等しいことを利用して三角形が相似であることを示します。
4. 合同と相似の証明
各三角形の合同や相似を利用して、三角形の辺の比率が等しいことを確認し、点 P, Q, R が一直線上に並ぶための条件を満たしていることを証明します。
よって、パスカルの定理が成立し、点 P, Q, R は必ず一直線上にあることが確認されます。
射影幾何学を用いた証明
1. 射影平面の設定
射影幾何学においては、ユークリッド平面を拡張し、無限遠点を含む射影平面を考えます。この平面では、すべての直線が交わり、平行線も無限遠点で交わるとされます。
2. 六角形の設定と対辺の延長
円錐曲線に内接する六角形 ABCDEF を射影平面上に配置します。対辺 AB と DE、BC と EF、CD と FA を延長し、それぞれの交点 P, Q, R を求めます。
3. 射影変換の適用
射影幾何学における射影変換を適用することで、円錐曲線を他の二次曲線に変換しながらも、直線上の関係性が保持されます。これにより、パスカルの定理の射影的な性質が確認されます。
4. デザルグの定理の利用
デザルグの定理を適用し、パスカルの定理が射影幾何学的な状況でも成立することを確認します。デザルグの定理は、二つの三角形が特定の条件下で射影的に対応する場合、それらの交点が一直線上にあることを示しています。
よって、射影幾何学においてもパスカルの定理が成立し、円錐曲線上にある六角形の対辺の延長の交点が一直線上に並ぶことが証明されます。
パスカルの定理の応用

パスカルの定理は、射影幾何学の基礎的な定理の一つであり、その応用は幾何学のみならず、現代の数学や物理学、さらにはコンピュータサイエンスにも及びます。以下では、パスカルの定理がどのように応用されているか、特に射影幾何学における位置づけと現代の応用例を見ていきます。
1. 射影幾何学における位置づけ
パスカルの定理は、射影幾何学において極めて重要な役割を果たしています。射影幾何学は、ユークリッド幾何学を拡張し、平行線が交わる無限遠点を導入した幾何学体系です。射影幾何学では、点、直線、円錐曲線の間に成り立つ関係性が研究されており、パスカルの定理はこの体系の中で二次曲線(円錐曲線)に関する重要な結果を提供します。
射影幾何学的観点からのパスカルの定理の意義:
- 直線と点の関係: パスカルの定理は、円や楕円、放物線など、円錐曲線に内接する六角形の対辺が交わる交点が必ず一直線上に並ぶことを示しており、これにより円錐曲線の基本的な射影的性質が明らかになります。
- デザルグの定理との関連: 射影幾何学におけるデザルグの定理(任意の平行四辺形で成り立つ直線と点の関係)と類似しており、デザルグの定理の二次曲線への一般化と考えることができます。これにより、射影幾何学における点と直線の双対性がさらに強調されます。
- 円錐曲線全体への拡張: パスカルの定理は円のみならず、楕円、双曲線、放物線などの他の円錐曲線に対しても適用でき、射影幾何学の普遍性を示す一例です。射影変換のもとで幾何学的性質が保持されるため、パスカルの定理の応用範囲は広範です。
2. 現代の数学における応用
パスカルの定理は現代数学の様々な分野で応用されています。特に、以下の分野でその影響が見られます。
(1) 代数幾何学
- パスカルの定理は、代数幾何学における曲線の特性を理解する上での基本的な手法として活用されます。円錐曲線やそれ以上の次数を持つ曲線の接線や交点に関する性質を解析する際、射影的なアプローチとしてパスカルの定理が適用されます。
- ベズーの定理やファイアーベッシュの定理など、他の重要な幾何学定理と組み合わせることで、代数幾何学的な問題を解決する際に使われます。
(2) トポロジーと解析学
- 射影幾何学を利用して、代数的トポロジーや複素解析における円錐曲線の研究に応用されています。特に、二次曲線の特性や交点に関する研究で、パスカルの定理の射影的性質が役立ちます。
(3) 数学教育
- パスカルの定理は、射影幾何学の基本定理の一つとして、中等教育から大学レベルの数学カリキュラムに組み込まれています。射影幾何学を学ぶことで、学生はユークリッド幾何学からさらに抽象的な幾何学体系への理解を深めることができます。
3. 現代の物理学における応用
パスカルの定理の幾何学的性質は、物理学の様々な分野にも影響を与えています。
(1) 光学
- パスカルの定理は、光の反射や屈折に関する問題、特にレンズやミラーを用いた光学系の設計において応用されています。光の経路を追跡する際に、射影幾何学の法則が利用され、特にレンズの設計における円錐曲線の性質が重要になります。
(2) 天文学
- 天文学では、二次曲線(特に楕円)が天体の軌道を表すため、パスカルの定理が惑星運動や軌道解析に役立っています。円錐曲線の射影的性質を利用して、天体の軌道の解析や予測に活用されています。
4. コンピュータサイエンスへの応用
(1) 画像処理とコンピュータビジョン
- パスカルの定理を含む射影幾何学は、画像処理やコンピュータビジョンの分野においても応用されています。特に、カメラで撮影された画像の視点変換や物体認識の際、射影変換や二次曲線に関する幾何学的性質が利用されます。パスカルの定理は、画像内の幾何学的な特徴点の関係を解析するための基本原理として使用されることがあります。
(2) 3Dモデリング
- 3次元空間のオブジェクトを平面に射影する際、パスカルの定理を含む射影幾何学の概念が活用されています。特に、3D空間での物体の位置関係を2次元の画像や画面に投影する際に、その射影関係を正確にモデル化するための数学的ツールとして利用されています。
パスカルの定理は、射影幾何学の基礎として広範囲に応用されており、数学、物理学、さらにはコンピュータサイエンスの分野で重要な役割を果たしています。射影幾何学における直線や点の関係性の理解を深めることで、他の多くの分野における問題解決にも貢献し続けています。
パスカルの定理と他の数学定理との関係
パスカルの定理は、射影幾何学や平面幾何学における他の定理と密接に関連しています。特に、ブリアンションの定理、メネラウスの定理、デザルグの定理との関連性は、幾何学的な構造を理解する上で重要です。以下に、これらの定理との比較や関連性について詳しく説明します。
1. ブリアンションの定理との関連
ブリアンションの定理(Brianchon's theorem)は、パスカルの定理の「双対」として知られています。双対性は射影幾何学の基本的な概念であり、点と直線の役割を入れ替えることで新たな関係を見出すことができます。
- ブリアンションの定理の内容:
パスカルの定理が「円に内接する六角形」に対するものであるのに対し、ブリアンションの定理は「円に外接する六角形」に関する定理です。具体的には、円に外接する六角形の対角線が3つの点で交わることを示します。ブリアンションの定理は次のように述べられます:円に外接する任意の六角形の3本の対角線は1点で交わる。
この定理は、パスカルの定理の双対的な性質を持ち、点と直線の間にある射影的な対応関係を示しています。
- パスカルの定理との双対関係:
パスカルの定理では、内接六角形の対辺の交点が一直線上に並ぶことを示していますが、ブリアンションの定理では、外接六角形の対角線が1点に交わるという、双対的な現象が成立します。この関係により、両定理は射影幾何学における点と直線の双対性を強調するものとなっています。
2.メネラウスの定理との比較
メネラウスの定理(Menelaus' theorem)は、三角形に対する重要な幾何学的定理であり、特に線分の比を用いて直線が三角形の辺をどのように交わるかを記述しています。パスカルの定理との関連性を理解するためには、メネラウスの定理の内容を押さえておくことが重要です。
メネラウスの定理の内容
三角形の辺に対して外部または延長された直線が交わるとき、その直線が三角形の3つの辺を連続的に交わる場合、以下の関係が成り立ちます:
( / ) × ( / ) × ( / ) = 1
ここで、点 , , は三角形 の各辺または延長上にあり、それらが一直線上にある場合、メネラウスの定理が適用されます。
パスカルの定理との類似点
パスカルの定理も、六角形の対辺の交点が一直線上にあることを示しています。この「一直線上に並ぶ」という点で、メネラウスの定理と類似していますが、メネラウスの定理は三角形に対するものであり、パスカルの定理は六角形(または円錐曲線に内接する多角形)に対するものです。
違い
- メネラウスの定理は、三角形の辺の比に基づいた関係式であり、直線が三角形の辺にどう交わるかに焦点を当てています。
- 一方、パスカルの定理は二次曲線上に内接する六角形の対辺に対して成立し、点と直線の射影的な性質に関するより一般的な定理です。
3. デザルグの定理との比較
デザルグの定理(Desargues' theorem)は、射影幾何学における基本的な定理の一つであり、パスカルの定理と同様に、直線や点の射影的な関係性を表しています。デザルグの定理は、射影平面における二つの三角形が特定の条件のもとで相似になることを示しています。
- デザルグの定理の内容:
二つの三角形が対応する頂点を結ぶ直線が一点で交わる場合、三角形の対応する辺の延長がすべて交わる点が一直線上に並びます。この直線はデザルグ線と呼ばれます。 - パスカルの定理との関連:
パスカルの定理は、六角形の対辺が交わる点が一直線上にあることを示しており、デザルグの定理の射影的な性質を拡張した形と見ることができます。どちらの定理も、射影幾何学における点と直線の関係性を扱っており、交点や直線の位置関係を解析する際に重要な役割を果たしています。 - 違い:
デザルグの定理は二つの三角形に対するものであり、射影平面上での相似や対応関係に焦点を当てています。一方、パスカルの定理は円錐曲線上に内接する六角形に対して成り立つ定理であり、円錐曲線に関する射影的性質に特化しています。
- ブリアンションの定理は、パスカルの定理の双対定理として、内接六角形と外接六角形の間にある双対的関係を示しています。
- メネラウスの定理は三角形に対する定理であり、パスカルの定理と同様に「点が一直線上に並ぶ」という性質に関連していますが、より比率に焦点を当てた定理です。
- デザルグの定理は、射影幾何学における三角形の相似性に基づく定理で、パスカルの定理の射影的性質と深く関連しています。
これらの定理はすべて、射影幾何学における基本的な構造を示しており、互いに補完し合いながら幾何学全体の理解を深める助けとなります。
パスカルの定理の拡張
パスカルの定理は、射影幾何学の強力な基礎定理の一つですが、元々は「円に内接する六角形」に適用されていました。この定理は一般化され、他の二次曲線や高次元空間においても成立することが示されています。以下では、パスカルの定理の拡張について詳しく説明します。
1. 一般的な場合への拡張
パスカルの定理は、円に内接する六角形に限定されず、すべての円錐曲線(楕円、双曲線、放物線)に適用可能です。これにより、円ではなく楕円や双曲線に内接する六角形にも同じ定理が成り立ちます。
- 円錐曲線への拡張:
円錐曲線とは、二次曲線である楕円、双曲線、放物線を含む曲線の総称です。これらの曲線上にある六つの点で構成される六角形でも、対辺を延長した際の交点が一直線上に並びます。この一般化により、パスカルの定理はユークリッド幾何学から射影幾何学へと適用範囲が広がります。 - 楕円や双曲線に内接する六角形:
楕円や双曲線上に選んだ6点から作成した六角形に対しても、同様に対辺の交点が一直線上に並びます。パスカルの定理は、これらのすべての円錐曲線に共通する幾何学的性質を記述しているため、射影的な性質が本質的に変わらないことを示しています。
2. 空間におけるパスカルの定理の拡張
パスカルの定理は、平面幾何学にとどまらず、空間幾何学にも拡張できます。この拡張により、三次元空間での曲線や多角形に関する新たな幾何学的性質が示されます。
- 空間パスカル定理:
二次曲線上にある6点が定義する空間六角形について、対応する対辺を延長すると、3つの交点が同一平面上に存在することが示されます。これにより、パスカルの定理は空間的な環境でも成立し、射影幾何学における三次元的な性質を反映しています。 - 射影空間幾何学の拡張:
射影幾何学では、二次元だけでなく高次元空間における点と直線、平面との関係が研究されています。パスカルの定理の空間への拡張は、この高次元幾何学の理論構築にも貢献し、三次元や四次元空間における多角形や多面体の構造理解を促進します。
まとめ
パスカルの定理の重要性
パスカルの定理は、初等幾何学における重要な発見から始まり、射影幾何学の中核を成す基本的な定理へと発展しました。その定理は、二次曲線(円錐曲線)の幾何学的性質を明確にし、点と直線の射影的な関係性を深く理解するための基礎を築きました。特に、デザルグの定理やブリアンションの定理といった他の定理との関連性から、射影幾何学の双対性や普遍性を強調しています。
さらに、パスカルの定理は現代数学の代数幾何学、解析学、トポロジー、さらには物理学やコンピュータビジョンの分野に至るまで、幅広い応用を持つ重要な理論です。
未来の研究に与える可能性
パスカルの定理は、未来の数学的研究においても重要な役割を果たす可能性があります。以下にそのいくつかのポイントを挙げます。
- 高次元空間における応用:
パスカルの定理は、射影幾何学の高次元化により、さらなる応用が期待されています。特に、代数幾何学における高次元曲面や空間における二次曲線の特性の研究に貢献し、幾何学の枠を超えた新たな分野での理論展開が可能です。 - 非ユークリッド幾何学との融合:
パスカルの定理は、非ユークリッド幾何学の世界でも適用可能であり、特に双曲幾何学やリーマン幾何学における曲線の研究にも応用が進むと考えられます。これにより、一般的な幾何学の理論にさらに広範な視点が加わるでしょう。 - 物理学や工学へのさらなる応用:
パスカルの定理は、光学系や天文学での応用がすでに行われていますが、今後の物理学や工学の発展に伴い、さらに複雑なシステムや構造の設計に応用される可能性があります。特に、量子力学や相対論的な物理学において、幾何学的性質がどのように作用するかの研究が進む可能性があります。
パスカルの定理は、その美しさと広範な応用の可能性を持つ定理であり、数学のさまざまな分野で今後も発展し続けるでしょう。

