
ベルヌーイの定理の基本的な概要
ベルヌーイの定理は、流体の運動において圧力、速度、位置エネルギーの関係を示す非常に重要な法則です。非圧縮性で粘性が無視できる理想流体が定常流れをしている場合、ある流線に沿った流体の圧力エネルギー、運動エネルギー、位置エネルギーの和は一定であることを述べています。
基本式
P + (1/2)ρv2 + ρgh = 定数
ここで:
- P は流体の圧力(単位:パスカル)
- ρ は流体の密度(単位:kg/m3)
- v は流体の速度(単位:m/s)
- g は重力加速度(9.81 m/s2)
- h は位置エネルギーに関連する高さ(単位:m)
この式は、流体の圧力が増加すると速度が低下し、逆に速度が増加すると圧力が低下するという、基本的な流体の性質を示しています。これにより、流体の動作に関する多くの現象を理解し、制御することが可能です。
定理の重要性と応用分野の紹介
ベルヌーイの定理は、流体力学の基礎原理として広く使用され、多くの分野に応用されています。特に以下のような実用的な分野があります。
航空工学
飛行機の翼の揚力を生むメカニズムは、ベルヌーイの定理で説明されます。翼の上面を通過する空気の速度が速くなることで圧力が低下し、下面の圧力との差圧が揚力を生み出します。この揚力が飛行機を空中に持ち上げる重要な要素となっています。
医療分野
酸素マスクや呼吸器における気流の制御も、ベルヌーイの定理を利用して設計されています。例えば、ヴェントリ効果を利用することで、少ない圧力差で効率的に酸素を供給することができます。
流体輸送システム
工業用パイプラインや給水システムなどにおいて、圧力差を利用して流体を移動させる際にもこの定理が用いられます。流体の速度と圧力のバランスを保つことで、安定した流れを確保し、エネルギー効率の向上を図ります。
流体力学や工学における役割
流体力学や工学において、ベルヌーイの定理は、流体の挙動を理解するための基本的な枠組みを提供します。特に、流体の速度と圧力の関係を定量的に捉えることができるため、設計や制御の場面で不可欠なツールとなっています。航空機の揚力、建物の換気システム、船舶の空力設計など、多くの工学分野でこの定理を利用して効率的な設計が行われています。
さらに、ベルヌーイの定理は、流体力学の他の理論と密接に関連しており、ニュートンの運動の法則や連続の方程式と組み合わせて利用することで、より精密なシミュレーションや解析が可能となります。これにより、現代の工学ではベルヌーイの定理を応用した数値流体力学(CFD)を駆使して、複雑な流体現象の解明や最適化を行っています。
これにより、ベルヌーイの定理は流体力学と工学の中心的な役割を果たし、多くの技術的な進歩に寄与しているといえます。
ベルヌーイの定理の歴史的背景
ダニエル・ベルヌーイと彼の業績
ダニエル・ベルヌーイ (Daniel Bernoulli, 1700-1782) は、スイス出身の数学者・物理学者であり、主に流体力学や統計学の分野で数多くの業績を残しました。彼はベルヌーイ家という、ヨハン・ベルヌーイやヤコブ・ベルヌーイなどの著名な数学者を多く輩出した一族に生まれ、科学の世界に早くから身を置いていました。
ダニエル・ベルヌーイは、医学を学びつつも物理学や数学に興味を持ち、特に流体力学に関する研究を進めていきました。彼の代表作である**『Hydrodynamica』(1738年)**は、流体の運動を数学的に解明した画期的な書物であり、この中で彼は「ベルヌーイの定理」として知られる法則を初めて提唱しました。この業績は、後の流体力学や航空工学の基礎を築くこととなり、彼の名を科学史に刻むことになります。
ベルヌーイの定理の発表とその時代背景
ダニエル・ベルヌーイがベルヌーイの定理を発表した18世紀は、物理学と数学の急速な発展期でした。ニュートンがその少し前に発表した『プリンキピア』が、力学における運動の法則を確立し、物体の運動に関する科学的理解が急速に深まりつつありました。ベルヌーイの定理は、ニュートンの運動法則を流体に適用した最初期の試みの一つであり、物体ではなく流体の運動の理解を大きく前進させました。
当時の科学界では、流体の性質や運動を定量的に説明する理論がほとんどなく、流体の力学に関する多くの疑問が残されていました。例えば、流体が圧力差や速度変化にどのように反応するのか、具体的な数式で説明できるモデルが求められていたのです。ダニエル・ベルヌーイは、流体が圧力、速度、高さの間でエネルギーを保存するという概念を導入し、これが「ベルヌーイの定理」として結実しました。
この定理の発表により、流体の運動が圧力、速度、位置エネルギーの相互作用に基づいて理解できることが示され、流体力学の理論的基礎が固められました。後に、蒸気機関やポンプ、飛行機の翼の設計など、さまざまな工学分野で広く応用されるようになりました。
他の科学者や定理に影響を与えた理論
ダニエル・ベルヌーイの業績は、同時代や後世の科学者に大きな影響を与えました。例えば、彼の父ヨハン・ベルヌーイや、アイザック・ニュートンなどの理論を踏まえながら、ダニエル・ベルヌーイは流体の運動に関する全く新しい視点を導入しました。特に、ニュートンの運動の法則を流体に適用し、それをエネルギー保存の原理と結びつけることで、流体の速度と圧力の関係を数学的に証明した点が画期的です。
また、後世の科学者たちもベルヌーイの定理を基礎に、多くの新しい理論を展開しました。例えば、レオンハルト・オイラーは、ベルヌーイの定理を発展させて流体の運動方程式を導出し、より広範な応用を可能にしました。また、19世紀に登場した熱力学や統計力学の分野でも、流体の運動を扱う際にベルヌーイの定理が用いられました。これにより、ベルヌーイの定理は、科学の多くの分野において基礎的な位置を占めるものとなりました。
ベルヌーイの定理は、ダニエル・ベルヌーイの卓越した洞察力と数学的手法によって生まれ、後の科学者たちによってさらに発展させられてきました。この定理は、流体力学だけでなく、工学、物理学、さらには現代の数値流体力学に至るまで、多くの科学技術分野に大きな影響を与え続けています。
ベルヌーイの定理の内容と数式
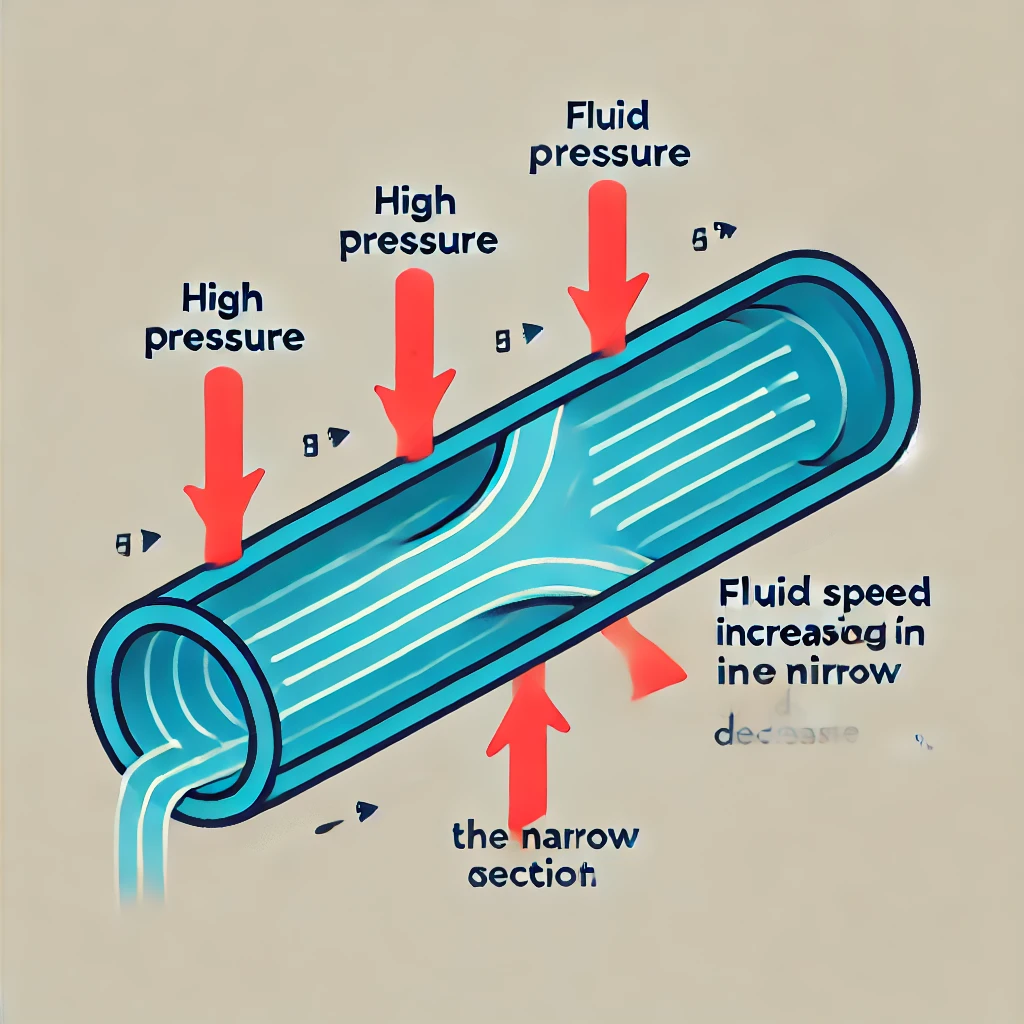
ベルヌーイの定理は、流体の運動において圧力、速度、位置エネルギーの関係を示す非常に重要な法則です。非圧縮性で粘性が無視できる理想流体が定常流れをしている場合、流線に沿った流体の圧力エネルギー、運動エネルギー、位置エネルギーの和は一定であることを示しています。
P + (1/2)ρv² + ρgh = 定数
ここで:
- P は流体の圧力(単位:パスカル、Pa)
- ρ は流体の密度(単位:kg/m³)
- v は流体の速度(単位:m/s)
- g は重力加速度(おおよそ 9.81 m/s²)
- h は基準点からの高さ(単位:m)
この方程式は、流体の総エネルギーが保存されることを表し、流体のある点での圧力エネルギー、運動エネルギー、位置エネルギーの和が一定であることを意味します。
各項の解説
圧力エネルギー P
圧力エネルギーは、流体の内部に働く力、すなわち流体が周囲に及ぼす圧力に関連します。この圧力は、流体が流れる方向に沿って働き、流体の運動を維持するために重要な要素です。
運動エネルギー (1/2)ρv2
流体の運動エネルギーは、流体が持つ速度に依存します。この項は、流速が大きくなると運動エネルギーが増加することを意味します。流体が速く流れる場所では、運動エネルギーが増加し、圧力が低下する関係があります。
位置エネルギー ρgh
位置エネルギーは、流体の高さに依存するエネルギーです。この項は、流体が重力の影響を受けている場合に特に重要です。流体が高い位置にあるほど、位置エネルギーは大きくなり、圧力エネルギーや運動エネルギーと相互に関係します。
定理の導出方法
ベルヌーイの定理は、エネルギー保存則に基づいて導かれます。これを簡単に説明するために、流線に沿って流れる微小な流体要素を考え、ニュートンの運動の第2法則(力と加速度の関係)とエネルギー保存則を組み合わせて導出します。
1. 運動の第2法則の適用
流体要素に働く力のバランスを考えます。流体が移動する際には、圧力の差と重力の影響が存在し、これらが流体の運動を支配します。流線に沿った流体要素における微小変化を扱うことで、力と運動エネルギーの関係を式に落とし込みます。
2. エネルギー保存の適用
流線に沿った各点において、流体の圧力エネルギー、運動エネルギー、位置エネルギーの総和が保存されるというエネルギー保存の原則を適用します。これにより、流体の運動に関する関係式が構築され、ベルヌーイの定理が導かれます。
3. 最終的な方程式の導出
最終的な方程式は以下の通りです。
P + (1/2)ρv² + ρgh = 定数
この定理は、流体が非圧縮性であり、粘性や摩擦力が無視できる場合に成立します。また、流線に沿って流れる流体において、各点でのエネルギーの総和が一定であることを表しています。
ベルヌーイの定理は、流体の運動に対する深い理解を与え、航空工学や水力学、建築設計など、多岐にわたる分野で応用されています。この定理により、速度と圧力の変化を予測し、効率的な流れの制御や設計が可能になります。
ベルヌーイの定理の前提条件
ベルヌーイの定理を適用するためには、いくつかの重要な前提条件があります。これらの条件が満たされない場合、定理は正確に適用できない可能性があります。以下は、ベルヌーイの定理を使用するための主な前提条件です。
1. 流体が非圧縮性であること
ベルヌーイの定理は、流体が非圧縮性であることを仮定しています。非圧縮性とは、流体の密度が流れの中で一定であることを意味します。これにより、流体の体積は圧力や温度の変化によってほとんど変化しないと仮定されます。この仮定が成り立つのは、通常は液体(例:水)や、低速で流れる気体です。高速で流れる気体や、圧縮性が高い場合には、ベルヌーイの定理はそのまま適用できません。
2. 摩擦や粘性のない理想流体であること
ベルヌーイの定理は、摩擦や粘性を無視できる理想流体に対して成り立つと仮定しています。現実の流体は、通常、流れの中で内部摩擦(粘性)を持っており、これによりエネルギー損失が生じます。しかし、ベルヌーイの定理ではこれを考慮せず、流体が摩擦や粘性を持たないと仮定します。このため、流体の運動エネルギーや圧力エネルギーが完全に保存されるという理想的な状況を想定しています。
3. 定常流れの仮定
ベルヌーイの定理は、流体が定常流れをしている場合に成り立ちます。定常流れとは、時間が経過しても流体の速度や圧力が一定であり、変動しない流れのことです。つまり、流体の各点での流速や圧力が時間的に変わらない状況を前提としています。これにより、エネルギー保存が成立し、流れ全体でのエネルギーが一定であるとみなせます。
ベルヌーイの定理の応用
ベルヌーイの定理は、さまざまな現象や技術に応用され、特に流体の圧力差と速度の関係を利用した設計や解析に役立ちます。以下に代表的な応用例をいくつか紹介します。
1. 飛行機の翼の揚力
ベルヌーイの定理の最もよく知られた応用例の一つは、飛行機の翼の揚力です。飛行機の翼は、上面が曲線を描き、下面は比較的平らな形状をしています。この形状により、翼の上を通る空気は下面よりも速く流れるため、上面の圧力が下がり、下面との圧力差が生じます。この圧力差が揚力を生み出し、飛行機が空中に持ち上げられるのです。ベルヌーイの定理により、この揚力のメカニズムを数学的に説明することができます。
2. 流体輸送管の圧力差
工業や建築の分野では、流体輸送管内での圧力差を利用して流体を効率的に移動させます。ベルヌーイの定理は、管内の流体の速度や圧力の変化を予測し、圧力差による流れの制御やパイプライン設計に役立ちます。例えば、上り坂に流体を輸送する際には圧力が必要であり、ベルヌーイの定理を用いて必要な圧力を計算することができます。
3. ヴェントリ効果と医療機器(酸素マスクなど)への応用
ヴェントリ効果は、流体が狭い通路を通る際に速度が増加し、圧力が低下する現象です。これはベルヌーイの定理に基づいています。この原理は、医療分野において、特に酸素マスクや呼吸器に応用されています。酸素を供給する際、ヴェントリ管を使用することで低圧力差で気体を効率よく患者に供給できるように設計されています。この技術により、患者が呼吸しやすい環境が整えられています。
4. 船の帆や車の空力設計
ベルヌーイの定理は、船の帆や自動車の空力設計にも応用されます。帆船の場合、風が帆を通過する際に速度の変化が生じ、圧力差が発生します。この圧力差により船が前進する力が生み出されます。車の空力設計では、車体の形状を工夫して空気抵抗を最小化し、効率的に速度を出すことができます。ベルヌーイの定理を用いて、車体の周りを流れる空気の速度と圧力を計算し、設計が最適化されます。
ベルヌーイの定理は、流体の挙動を定量的に捉え、現代の航空、医療、工業、建築など、さまざまな分野で応用されています。
よくある誤解

ベルヌーイの定理と飛行機の揚力の誤解
飛行機の揚力に関する一般的な誤解の一つは、ベルヌーイの定理だけが揚力を説明しているというものです。よく紹介されるのは、翼の上側を流れる空気の速度が速くなることで圧力が下がり、下側との差圧によって揚力が生じるという説明です。この説明自体は正しいものの、完全ではありません。実際には、翼の角度や空気の流れの方向も揚力に大きな影響を与えており、ベルヌーイの定理だけで説明できるものではないのです。
特に、翼の迎え角(気流に対する翼の角度)によって、下側の空気は翼に押し付けられ、揚力が発生するという現象があり、これが次の項で説明するニュートンの運動の第3法則と密接に関係しています。
他の力(ニュートンの運動の第3法則)との関係
揚力の形成には、ベルヌーイの定理だけでなく、ニュートンの運動の第3法則(作用・反作用の法則)も大きく関与しています。ニュートンの法則によれば、翼が空気を下方に押し付けると、反作用として空気が翼を上方に押し上げる力が生じます。これにより、飛行機は揚力を得て飛行します。
したがって、飛行機の揚力を完全に説明するためには、ベルヌーイの定理による圧力差とニュートンの第3法則による力の作用・反作用の両方を考慮する必要があります。この2つの原理が揃って初めて、揚力が成立するのです。
ベルヌーイの定理と現代の発展

定理を超えた現代の流体力学の理論
現代の流体力学では、ベルヌーイの定理は依然として重要な役割を果たしていますが、より複雑な流体現象や高精度な設計を行うために、新しい理論や技術が発展しています。例えば、圧縮性流体や乱流といった現象は、ベルヌーイの定理の適用範囲を超えており、これらに対処するためには他の数式モデルや理論が必要です。
また、粘性の影響や、現実の流れで発生する摩擦力を考慮したナビエ・ストークス方程式も、現代の流体力学で頻繁に用いられています。この方程式は、ベルヌーイの定理が前提とする理想流体の仮定を超えて、実際の流体の挙動を詳細に記述することが可能です。
CFD(数値流体力学)とシミュレーション技術
現代の工学における重要な発展の一つが、CFD(数値流体力学)の技術です。CFDは、コンピュータシミュレーションを用いて流体の挙動を数値的に解析する技術で、ベルヌーイの定理やナビエ・ストークス方程式などの基礎理論を基に、複雑な流体の流れを詳細にシミュレーションできます。
これにより、従来の理論では難しかった複雑な設計や最適化が可能になり、飛行機や自動車、建築物、さらには医療機器まで、様々な分野での設計・開発が飛躍的に進展しました。
新しい工学設計や研究への貢献
ベルヌーイの定理を基盤とした流体力学の進展により、新しい工学設計が可能になっています。特に、航空工学やエネルギー分野、建築の空力設計などでの設計の効率化が進み、燃費の向上や風力発電機の最適化など、環境に優しい技術にも貢献しています。
また、流体のシミュレーション技術を用いることで、より精密な構造物の設計や、効率的な流体輸送のシステム構築が可能になり、これらの技術革新が多くの産業に大きな影響を与えています。
まとめ
ベルヌーイの定理の重要性の再確認
ベルヌーイの定理は、18世紀に提唱された古典的な理論でありながら、現在でも流体力学や工学の基礎として非常に重要な役割を果たしています。圧力と速度、位置エネルギーの関係を定式化することで、流体の運動を定量的に理解できるため、航空機の設計から配管システム、さらには医療機器まで、幅広い分野で応用されています。
現代における定理の位置づけとその進化
現代では、ベルヌーイの定理はさらに発展し、数値流体力学(CFD)やナビエ・ストークス方程式などの新しい理論と技術と組み合わせて使われています。これにより、より複雑な流体現象の理解や、精密な工学設計が可能となり、技術の進化に大きく貢献しています。
したがって、ベルヌーイの定理は、現代の流体力学や工学設計において欠かせない基礎的な理論であり、今後も様々な分野でその応用が期待されます。また、シミュレーション技術の発展により、今後さらに複雑な流れや現象の解析に貢献していくでしょう。

