チェバの定理とは何？証明や応用などわかりやすく解説！

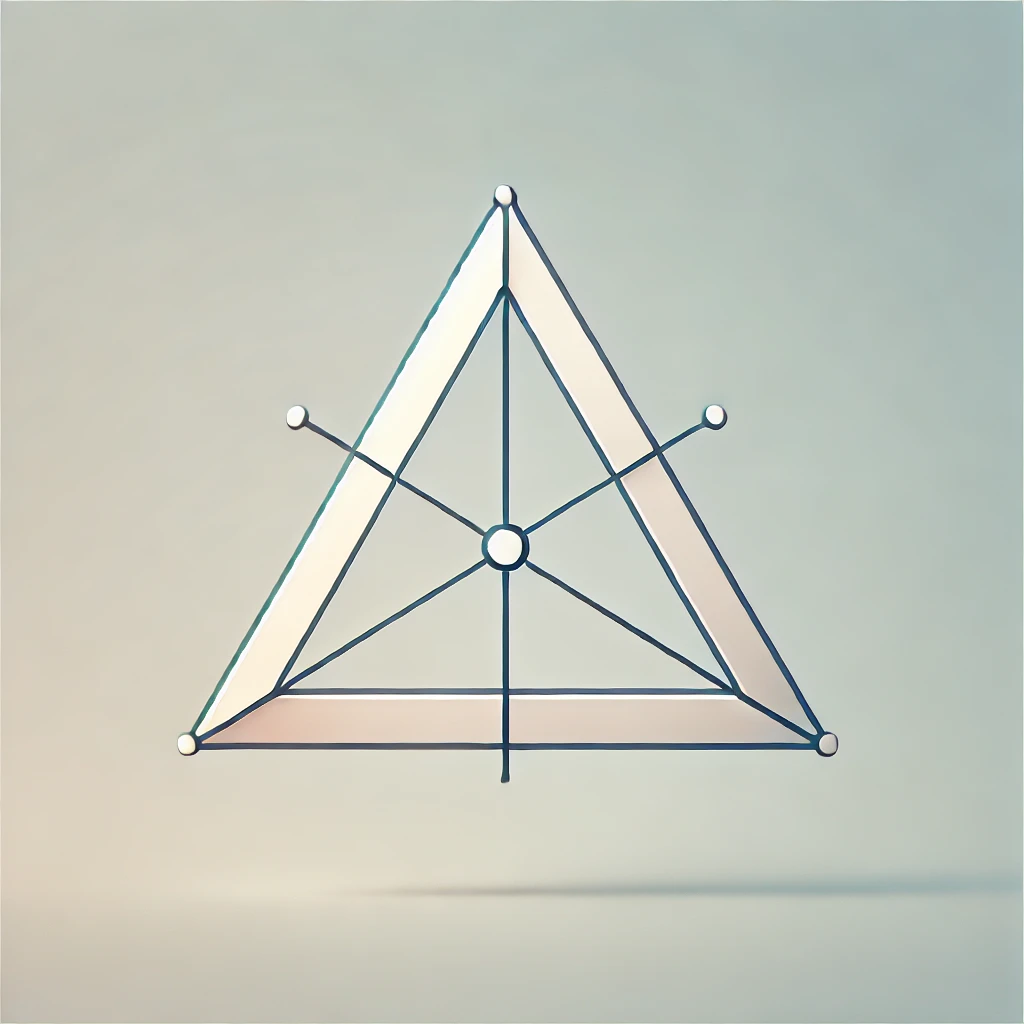
チェバの定理は、平面幾何学の重要な定理で、三角形の各頂点から対辺に向かって引かれた線（これを「チェバ線」と呼びます）が一点で交わるための条件を示しています。

具体的には、三角形の頂点を A, B, C とし、各頂点から対辺に線を引きます。これらの線は、対辺上の点 P, Q, R を通ります。チェバの定理によれば、これら3本の線が一点で交わるためには、次のような条件が必要です。

• 線 AP が辺 BC を点 P で分割する場合の比を AP/PB とします。
• 線 BQ が辺 CA を点 Q で分割する場合の比を BQ/QC とします。
• 線 CR が辺 AB を点 R で分割する場合の比を CR/RA とします。

これらの比を掛け合わせた結果が 1 になるとき、3本の線は必ず一点で交わります。つまり、以下の条件が成り立ちます。

(AP ÷ PB) × (BQ ÷ QC) × (CR ÷ RA) = 1

この条件が成り立つことで、チェバの定理が成立します。

チェバの定理の重要性

チェバの定理は、幾何学における三角形の問題を解くための強力なツールです。この定理の興味深い点は、逆定理が成立することです。すなわち、3本の線が一点で交わるためには、三角形の各辺が特定の比率で分割されている必要があります。この逆定理は、幾何学的な配置問題を解決する上で非常に役立ちます。

さらに、チェバの定理は、他の幾何学的な定理、特にメネラウスの定理とも関連しています。これらの定理を組み合わせることで、複雑な三角形の問題を解くことが可能になります。

教育現場での利用

チェバの定理は、そのシンプルさから、教育現場で幾何学を学ぶ上で非常に役立ちます。特に、三角形内の線分の交点や比率に関する問題を理解するための基本的なツールとして使用されます。学生にとっては、幾何学的証明の基礎を学ぶ上で重要な例題となります。

 

チェバの定理の歴史的背景

ジョヴァンニ・チェバ (Giovanni Ceva): 定理の発見者

チェバの定理は、17世紀のイタリアの数学者であるジョヴァンニ・チェバ（Giovanni Ceva）によって発見されました。彼は1647年12月7日にイタリアのミラノに生まれ、1690年に有名な著作『Geometria Motus（動力幾何学）』を発表するなど、幾何学分野で重要な貢献を果たしました。
チェバは、主に力学と幾何学に興味を持っており、その研究の過程で「チェバの定理」として知られる結果を導きました。彼の業績は、現代の幾何学だけでなく、物理学や力学にも影響を与え、彼の考え方は力の均衡に関する問題の解決にも役立ちました。

発見の経緯

チェバの定理は、彼の著作『De Lineis Rectis（直線に関する考察）』で最初に紹介されました。この書物は1678年に発表され、チェバはこの中で、三角形の頂点から対辺に向かって引かれた線が一点で交わるための条件を詳細に説明しています。彼はこの発見を、古代ギリシャの数学者たちが行った幾何学の研究を発展させる形で導き出しました。

チェバは、古代ギリシャのメネラウスの定理と呼ばれる別の定理からインスピレーションを得ました。メネラウスの定理は、三角形の外部に引かれた直線が特定の条件を満たす場合に成り立つものです。チェバは、この定理を三角形の内部に適用することで、三角形の頂点から引かれた内部の線が一点で交わる条件を証明しました。この発展は、当時の幾何学の研究に新たな視点を提供し、後の数学者たちにも多くの影響を与えました。

また、チェバが生きた時代は、科学と数学が大きく進展していた時期であり、ガリレオ・ガリレイやアイザック・ニュートンといった他の科学者たちが自然現象の数理モデル化に取り組んでいました。チェバもこの知的な潮流の中で活動し、力学と幾何学の融合を追求しました。彼の幾何学的な視点は、後に力学の平衡条件に関する理論にも応用され、現代の静力学においてもその概念が生かされています。

チェバの定理は、後世の数学者たちによりさらに洗練され、教育や研究の場で頻繁に使用される基本的な幾何学の定理として確立されました。

定理の内容（公式）

チェバの定理の公式

チェバの定理は、三角形において、各頂点から対辺に引かれた3本の線（チェバ線）が一点で交わるための条件を示しています。この条件は、三角形の頂点とその対辺上の交点における比率の関係式として表されます。

具体的には、次のような状況を考えます。三角形 ABC があり、頂点 A、B、Cからそれぞれ対辺 BC、CA、AB に向けて線を引き、交点を P、Q、Rとします。チェバの定理によると、これらの3本の線 AP、BQ、CR が一点で交わるためには、次の関係が成立する必要があります。

(AP ÷ PB) × (BQ ÷ QC) × (CR ÷ RA) = 1

この式において、次のことを意味しています。

• APは頂点 A から対辺 BC 上の点 P までの線分の長さ、
• PBは点 P から頂点 B までの線分の長さ。

同様に、

• BQは頂点 Bから対辺 CA上の点 Qまでの線分の長さ、
• QCは点 Qから頂点 Cまでの線分の長さ、
• CR は頂点 Cから対辺 AB 上の点 R までの線分の長さ、
• RAは点 Rから頂点 Aまでの線分の長さです。

これらの比率が成り立つとき、3本の線は必ず一点で交わります。逆に、この条件が満たされている場合、その3本の線は共通の一点で交差します。

比の関係式の説明

チェバの定理は、三角形の内部における点の位置とその比率に関する定理です。たとえば、比 (AP ÷ PB) は、三角形の頂点 $A$ から引かれた線が対辺 $BC$ を分割する位置を示しています。他の2つの辺についても同様に比で表すことで、これらを掛け合わせた値が1になると、3本のチェバ線が一点で交わることが確認できます。

この関係式は、三角形の辺が特定のバランスで分割されるときに成立します。つまり、三角形の3つの辺が特定の比率で分割されるために、3本のチェバ線が共通の点で交わることを「幾何学的な対称性」として表しています。

定理が適用される三角形の条件

チェバの定理が適用されるためには、三角形が通常の形状をしており、各頂点から対辺に引かれるチェバ線が存在する必要があります。これにより、以下の条件が成立します。

1. 三角形の内部における交点: 3本のチェバ線が三角形の内部で交差する場合、この交点は必ず1つである。
2. 外心や内心との関連性: チェバ線が三角形の特定の中心（例えば、重心、内心、外心）に向かう場合にも、チェバの定理が応用され、三角形の対称性に関する問題を解くのに役立ちます。

このように、チェバの定理は、三角形の特定の交点や比率に関する幾何学的問題を解決するための強力なツールです。

チェバの定理の証明

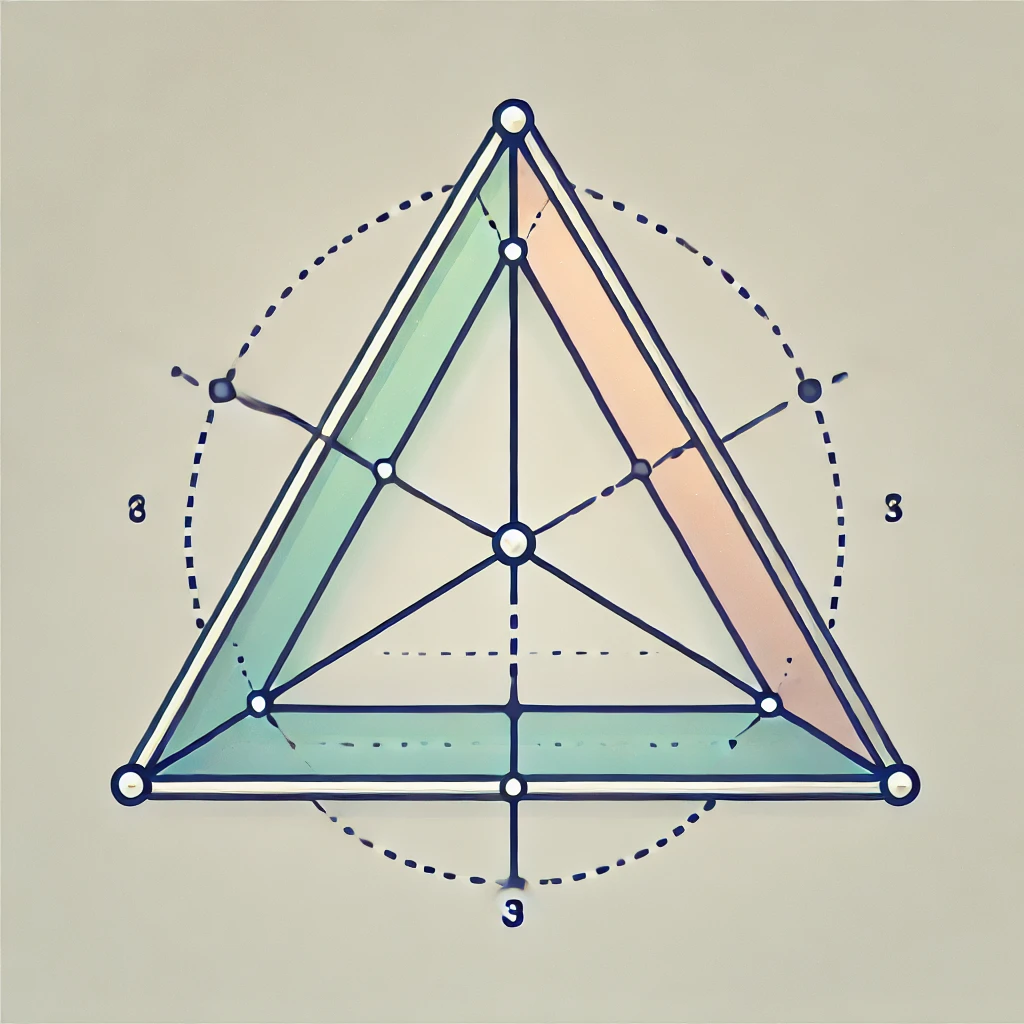
チェバの定理の証明には、大きく分けて2つの方法があります。1つは幾何学的証明で、図形的な性質を使って証明します。もう1つは代数的証明で、三角形の頂点の座標や線の比率を使って数式的に証明します。ここでは、各証明方法をステップごとに説明します。

1. 幾何学的証明

ステップ1: 三角形内でのチェバ線の定義
三角形 ABCを考えます。各頂点 A、B、C から、それぞれ対辺 BC、CA、ABに向けて線分を引きます。これらの線分は、それぞれの辺を分割し、交点を P、Q、Rとします。これらの線分を「チェバ線」と呼びます。チェバの定理は、この3本のチェバ線が一点で交わる条件を示しています。

ステップ2: 面積比の利用
次に、三角形の面積に注目します。三角形 ABC の中で、チェバ線が各頂点に隣接する小さな三角形を作ります。例えば、三角形 APBと三角形 PBC の面積比は、対応する辺の長さの比に比例します。以下の関係が成り立ちます。

• (三角形 APC の面積)÷(三角形 PBC の面積)=AP÷PB
• (三角形 BQA の面積)÷(三角形 CQA の面積)=BQ÷QC
• (三角形 CRB の面積)÷(三角形 ARB の面積)=CR÷RA

これらの面積比を掛け合わせると、次の式が得られます。

(AP ÷ PB) × (BQ ÷ QC) × (CR ÷ RA) = 1

ステップ3: 総面積の比による証明
この式は、3本のチェバ線が三角形の内部で一点に交わるための条件を示しています。つまり、面積比に基づいて、チェバ線が一点で交わることが証明されました。

2. 代数的証明

ステップ1: 座標系の設定
代数的証明では、まず三角形の頂点 $A$、$B$、$C$ の座標を設定します。たとえば、次のように座標平面上に三角形を配置します。

• A(0,0)
• B(1,0)
• C(0,1)

これにより、三角形の幾何学的な性質を代数的に取り扱う準備が整います。

ステップ2: 点の分割比の導入
次に、チェバ線が対辺をどのように分割するかを数学的に表現します。例えば、頂点 $A$ から引かれた線 $AP$ が対辺 $BC$ 上の点 $P$ をどのように分割するかは、次のように表せます。

• AP÷PB=k1​

他の頂点 $B$ から対辺 $CA$ に引かれた線についても、次のように表します。

• BQ÷QC=k2​
• CR÷RA=k3​

ステップ3: 比率の導出
これらの比率 k1、k2、k3を掛け合わせた結果が1であれば、3本のチェバ線が一点で交わることが証明されます。つまり、次の式が成り立ちます。

k_1 × k_2 × k_3 = 1

ステップ4: 比の計算
各頂点での分割比を具体的な値に代入し、この条件が成立することを確認します。これにより、代数的にチェバの定理が証明されます。

証明のまとめ

• 幾何学的証明では、三角形の面積比に基づいてチェバの定理を証明します。
• 代数的証明では、座標と分割比を利用して、数学的にチェバの定理の条件が成り立つことを示します。

どちらの方法でも、チェバの定理が正しいことを証明できますが、幾何学的証明は直感的な理解を助け、代数的証明はより厳密な数理的な証明となります。

​

チェバの定理の応用

チェバの定理は、三角形の内部で線の交点の位置や、三角形の辺の比を特定する際に使われます。ここでは、チェバの定理を使った具体的な問題を紹介します。

応用例題

三角形ABCの各頂点から対辺に線を引きます。
頂点Aから引いた線は辺BC上の点Pで交わり、
頂点Bから引いた線は辺CA上の点Qで交わり、
頂点Cから引いた線は辺AB上の点Rで交わるとします。

これらの線が一点で交わるかどうかを、チェバの定理を使って確認します。

---

解答

三角形の各頂点から引かれた線が一点で交わるための条件は、チェバの定理により次のように表されます。

AP ÷ PB × BQ ÷ QC × CR ÷ RA = 1

この条件に基づいて、各線分の長さの比を代入して計算します。

---

具体例

次のような比率が与えられているとします。

AP ÷ PB = 2
BQ ÷ QC = 3
CR ÷ RA = 1 ÷ 6

これらの比率を掛け合わせると、

2 × 3 × (1 ÷ 6) = 1

したがって、これらの線は一点で交わることが確認できます。

メネラウスの定理との関係

チェバの定理は三角形の内部における交点を扱いますが、メネラウスの定理は三角形の外部にある直線が三角形の各辺と交わる場合に適用されます。メネラウスの定理も、三角形の辺の比に基づいていますが、適用される状況が異なります。両方の定理を組み合わせることで、三角形に関する複雑な問題も解決することができます。

関連性の理解

チェバの定理は三角形の内部に適用され、メネラウスの定理は三角形の外部に適用されるという違いがありますが、どちらの定理も三角形の辺の比に基づいています。これらを組み合わせることで、複雑な三角形の問題を解決することができます。

例えば、チェバの定理を用いて内部の交点を特定し、その結果を利用してメネラウスの定理で外部の点の位置関係を解くことが可能です。

このように、チェバの定理とメネラウスの定理は、幾何学における三角形の問題解決において補完的に活用されます。特に三角形の内部外部を問わず、線や点の位置関係を扱う問題で、両方の定理を組み合わせることで広範囲な応用が可能です。

チェバの定理の発展と現代的応用

現代数学への応用

チェバの定理は、古典幾何学における基本的な定理として知られていますが、現代数学においても様々な応用が見られます。特に、プロジェクティブ幾何学や幾何学的最適化の分野で活用されています。

• プロジェクティブ幾何学では、点や線の交点の性質が重要なテーマであり、チェバの定理は点や直線の交点に関する問題に利用されます。プロジェクティブ平面上での線の交差条件や交点の位置関係を研究する際に、この定理が役立ちます。
• 幾何学的最適化においては、三角形や多角形の重心や対称性を考慮する問題にチェバの定理が応用されます。例えば、建物や橋の構造設計において、力が均等に分配される最適な構造を見つける際に、チェバの定理を使って安定性を考慮した配置を検討します。

関連する応用分野

チェバの定理は、数学以外の分野にも応用が広がっています。以下は、特に現代において注目される応用分野です。

• コンピュータサイエンスでは、三角形分割やグラフィックス処理においてチェバの定理が役立ちます。3Dモデリングやレンダリングの際、三角形の内部分割や交点の計算が必要となる場合、チェバの定理を用いて効率的に処理を行うことが可能です。特に、三次元空間における交点や交差を扱うシステムの設計に応用されています。
• コンピュータグラフィックスやゲーム開発でも、キャラクターモデリングや物理エンジンにおいて、物体の形状を細かく制御するためにチェバの定理が利用されます。複雑な物体のアニメーションや物理的な挙動をシミュレートする際、三角形の分割や点の交点を計算するためのツールとして定理が使われています。
• ロボティクスでは、物体の持ち方や操作の際、重心や力の分布を考慮した設計にチェバの定理が応用されます。特に、3点の支点を持つロボットアームなどで、安定性を考慮した設計に役立ちます。

まとめ

チェバの定理の重要性の再確認

チェバの定理は、三角形の各頂点から対辺に引かれた線が一点で交わるための条件を示す幾何学の基本的な定理であり、その証明や応用を通して、古典幾何学だけでなく現代の数学や様々な分野において重要な役割を果たしています。この定理を通じて、幾何学的な図形の特性や、物理的な力の均衡に関する問題を効率的に解くことができます。

さらに、メネラウスの定理やプロジェクティブ幾何学との関連性を考慮すると、チェバの定理は単なる古典幾何学の結果に留まらず、現代の数学や工学、コンピュータサイエンスの問題にも幅広く応用できる強力なツールとなっていることが分かります。

今後の研究課題

チェバの定理に関連する今後の研究や応用の可能性としては、以下の点が挙げられます。

• 幾何学的アルゴリズムの最適化：チェバの定理を利用して、コンピュータサイエンスやグラフィックスにおける三角形分割の効率化や、交点計算の精度向上を図ることが期待されます。
• ロボティクスやAIへの応用：複雑な物体の動きや安定性を考慮した設計にチェバの定理を応用する研究が進むことで、より安定したロボットや自律システムの開発が可能になるでしょう。
• 教育へのさらなる応用：チェバの定理は、幾何学教育においても強力な教材となり得ます。特に、学生に直感的に幾何学の概念を教えるための問題集やソフトウェアに組み込まれることで、定理の理解を深める機会が広がります。

チェバの定理は、単なる古典幾何学の枠を超えて、様々な分野でさらなる発展と応用が期待される重要な定理であると言えます。

ピタゴラスの定理とは何？証明や数式などわかりやすく解説！