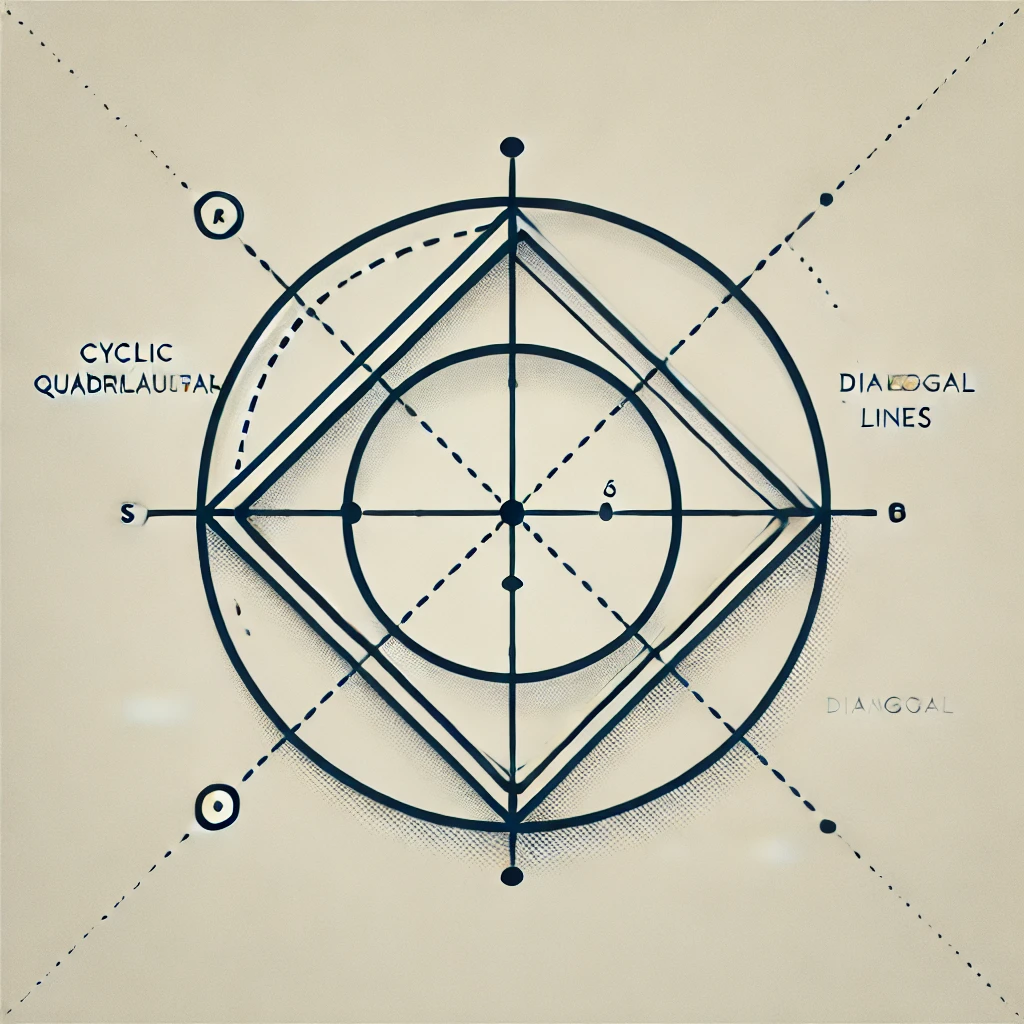
トレミーの定理の概要
トレミーの定理(Ptolemy's Theorem)は、古代ギリシャの数学者クラウディオス・プトレマイオス(Ptolemy)が発見した幾何学の定理で、円に内接する四辺形に関する重要な性質を記述しています。この定理は、円周上にすべての頂点が配置された四辺形(内接四辺形)の辺と対角線の間に特定の関係が成り立つことを示しています。
この定理は、図形幾何学における強力なツールであり、特に三角法や天文学の計算において、歴史的に重要な役割を果たしました。トレミーの定理は、単に四辺形の辺や対角線の長さを結びつけるだけでなく、円に関連する多くの幾何学的現象を理解するための基礎を築きました。
定理が扱う内容や基本的な性質の紹介
円に内接する四辺形 A, B, C, D があるとき、対角線 AC と BD の積は、辺 AB, CD, AD, BC の積の和に等しくなります。次の式が成り立ちます。
AC × BD = AB × CD + AD × BC
ここで、円に内接していない任意の四辺形ではこの等式は成立しませんが、内接四辺形では常に成り立つのが特徴です。この性質を利用することで、幾何学的な証明や問題解決において、対角線や辺の長さを計算する際に大きな助けとなります。
主なポイント:
- 定理は、円に内接する四辺形にのみ適用されます。
- 四辺形の辺と対角線が特定の関係式に従うという性質を示します。
- 定理を利用することで、円周角や内角を持つ図形に対する高度な解析が可能です。
定理の歴史的背景:トレミーとは誰か?
クラウディオス・プトレマイオス(Claudius Ptolemy、85年頃〜165年頃)は、古代ローマ時代のギリシャ系の天文学者、数学者、地理学者です。彼はアレクサンドリアで活躍し、特に天文学と地理学の分野で後世に大きな影響を与えました。彼の代表作である『アルマゲスト』は、天文学の古典的な理論を集大成し、約1,400年にわたってヨーロッパとイスラム世界で参照されました。
プトレマイオスは、天文学において地球中心の宇宙モデル(プトレマイオスモデル)を提唱し、このモデルは後にコペルニクスの地動説が広まるまで広く信じられていました。また、彼は三角法の基礎を築く上で重要な貢献をし、特に円周上の点に関する幾何学的関係を分析するために、彼の定理を活用しました。
彼の研究の多くは、ギリシャの数学者や天文学者であるヒッパルコスに基づいていましたが、彼自身の貢献も極めて重要です。トレミーの定理もその一つで、彼の名前が冠された定理として後世に伝えられ、現代でも数学や物理学において使われています。
トレミーの定理の定義
四辺形に対するトレミーの定理の内容
トレミーの定理は、円に内接する四辺形に関する幾何学的な関係を示す定理です。内接四辺形とは、すべての頂点が円周上に存在する四辺形のことです。この定理は、四辺形の対角線と各辺の長さが特定の関係式で結びついていることを表しています。
円に内接する四辺形の対角線と辺の関係式
トレミーの定理によると、円に内接する四辺形において、対角線の積は隣接する2つの辺の積と、反対側の2つの辺の積の和に等しくなります。
円に内接する四辺形 ABCD に対して、対角線 AC と BD、および各辺 AB、BC、CD、DA の長さには次の関係式が成り立ちます:
AC × BD = AB × CD + AD × BC
ここで、AC と BD は四辺形の対角線の長さ、AB、BC、CD、DA は各辺の長さを表します。
数式での表現
トレミーの定理は次のように数式として表されます:
AC × BD = AB × CD + AD × BC
この関係式は、円に内接する四辺形に対してのみ成立します。円に内接していない四辺形では成立しません。この定理は、円周角の性質や他の幾何学的な定理とも深く関連しており、三角法や円に関する問題の解決において非常に有用です。
トレミーの定理の証明

トレミーの定理を証明するためには、基本的な幾何学の知識を使い、特に三角形の相似や余弦定理を利用します。ここでは、円に内接する四辺形 ABCD の対角線と辺の関係を証明していきます。
証明の流れ
- 円周角の性質の利用
- 三角形の相似の導入
- 余弦定理を使った関係式の導出
- トレミーの定理の成り立ちの確認
証明のステップ
1. 円に内接する四辺形の基本性質
まず、円に内接する四辺形 ABCD では、各頂点 A, B, C, D が同一の円周上にあります。この性質により、円周角の定理を適用できます。円周角の定理によると、弧 AB に対する角度は、点 A と C で等しい円周角を形成します。
2. 三角形の相似の導入
次に、対角線 AC と BD が交わる点を P とします。これにより、三角形 APB と DPC、および三角形 APD と BPC を考えることができます。これらの三角形は相似です。次の対応する角度が等しいためです:
- ∠APB = ∠DPC(対頂角)
- ∠ABP = ∠DCP(円周角の定理により等しい)
この三角形の相似性を利用して、各辺の比が対応することがわかります。
3. 余弦定理の使用
次に、余弦定理を使って対角線と辺の間に関係を導きます。円に内接する四辺形における余弦定理に基づいた計算により、次の関係式が得られます。
対角線 AC と BD が交わる点 P における相似三角形の性質に基づき、辺の積に関する式を導き出します。
4. トレミーの定理の関係式
これまでのステップを踏まえ、相似な三角形と余弦定理を用いることで、次の関係が得られます:
AC × BD = AB × CD + AD × BC
これはトレミーの定理そのものです。
図形を用いた視覚的な説明
証明の中では、以下の図を使って説明することが理解を助けます:
- 円に内接する四辺形 ABCD
- 対角線 AC と BD の交点 P
- 相似三角形 APB と DPC、および APD と BPC の対応関係
この図により、各角度や辺の関係を視覚的に確認しながら証明を進めることができます。
以上の証明を通じて、トレミーの定理が円に内接する四辺形において、対角線と辺の長さの間に特定の関係があることが示されました。この証明は、基本的な幾何学の性質、特に三角形の相似や余弦定理を活用しており、幾何学の多くの問題に応用できます。
トレミーの定理の応用例
トレミーの定理は、円に内接する四辺形における対角線と辺の関係を示す幾何学的な定理であり、さまざまな問題解決や現代の数学・物理学において応用されています。以下はその具体的な応用例です。
幾何学的問題の解決における応用
トレミーの定理は、古典的な幾何学において、円や多角形に関連する問題の解決に使用されます。特に、円に内接する図形の辺の長さや対角線の長さを求める問題において有用です。
例えば、次のような幾何学的問題が考えられます:
- 四辺形の辺の長さの特定:ある円に内接する四辺形の3つの辺の長さが分かっている場合、残りの1つの辺や対角線の長さをトレミーの定理を利用して求めることができます。
- 対角線の長さの計算:円に内接する四辺形における2つの対角線の長さが必要な場合も、辺の長さが分かっていればトレミーの定理に基づいて計算が可能です。
これらのように、円周を基にした図形の解析にはトレミーの定理が非常に役立ちます。
三角形や多角形に対する解析
トレミーの定理は、三角形や多角形の解析にも応用できます。特に、以下のような幾何学的な場面で利用されています:
- 三角形の解析:円に内接する四辺形は、基本的に2つの三角形に分解して考えることができるため、三角形の解析にも応用できます。たとえば、余弦定理や相似性を利用して、三角形の辺と角度の関係をより深く解析することができます。
- 多角形の解析:多角形が円に内接している場合、その辺や対角線の関係をトレミーの定理を使って解析できます。特に、正多角形の場合、辺の比率を基にして対角線や外接円に関する性質を調べることができます。
現代の数学や物理学における利用
トレミーの定理は、現代の数学や物理学でも応用されています。特に、三角法や解析幾何学の分野において次のような場面で利用されています:
- 球面幾何学:球面上の図形の解析において、トレミーの定理は三角法の一部として利用されます。特に、球面三角法では、地球上の距離や角度の計算において、この定理に基づく概念が応用されています。
- 解析幾何学:幾何学的な構造を解析する際に、特定の対角線や辺の関係をトレミーの定理を用いて計算することで、より複雑な図形の性質を理解することができます。
円に関する問題やコンピュータービジョンでの応用
トレミーの定理は、円に関連する多くの問題において実用的です。たとえば、次のような応用があります:
- 円周上の点に対する解析:コンピュータービジョンや画像処理では、円や円弧に関連する問題が頻繁に発生します。円周上の複数の点に関する関係式を求める際に、トレミーの定理が役立つことがあります。特に、形状認識や物体のトラッキングにおいて、対象物の輪郭を円として捉える場面で利用されます。
- コンピュータービジョン:3D空間における物体の認識やトラッキングのための幾何学的計算において、トレミーの定理を基にしたアルゴリズムが使用されることがあります。物体の位置関係や回転に関連する問題において、幾何学的な関係を理解するために役立ちます。
トレミーの定理は、古典幾何学から現代の物理学、コンピュータービジョンに至るまで、多岐にわたる分野で応用されています。その精緻な数式と明確な幾何学的関係は、特に円や四辺形の解析において強力なツールとして機能し、実際の問題解決においても重要な役割を果たしています。
トレミーの定理と他の幾何学定理の関係

トレミーの定理は、円に内接する四辺形(サイクル四辺形)に関する基本的な定理です。これを理解するには、サイクル四辺形や余弦定理との関連を考えることが重要です。ここでは、トレミーの定理をそれらの定理と比較し、さらにどのように発展して応用されるかを説明します。
1. サイクル四辺形との関係
トレミーの定理は、サイクル四辺形(円に内接する四辺形)に対して成立する定理です。サイクル四辺形には以下のような性質があります。
- 対角線の交点で形成される角度の和は180度です。
- 対角線は外接円の中心を通るか、交点は円の内部にあります。
トレミーの定理は、これらの性質に基づき、サイクル四辺形の辺と対角線の長さの関係を次のように示しています。
AC × BD = AB × CD + AD × BC
この定理はサイクル四辺形にのみ適用され、円に内接していない四辺形には適用されません。
2. 余弦定理との比較
余弦定理は、三角形において辺の長さと角度の関係を示す定理です。三角形 ABC において、次の関係が成り立ちます。
c² = a² + b² - 2ab × cos(C)
ここで、a、b、c は三角形の辺の長さ、cos(C) は角度Cの余弦です。余弦定理は任意の三角形に適用でき、特に非直角三角形の解析に役立ちます。
トレミーの定理と余弦定理には次のような類似点と違いがあります。
- 類似点:どちらも辺と角度の関係を扱います。トレミーの定理は四辺形の辺と対角線の関係、余弦定理は三角形の辺と角度の関係を示しています。
- 違い:余弦定理は任意の三角形に適用できますが、トレミーの定理は円に内接する四辺形にのみ適用されます。
両定理は、特に円に関する問題や三角法に関連する問題を解く際に補完的に使われます。
3. トレミーの定理の発展形と応用
3.1 球面幾何学におけるトレミーの定理
トレミーの定理は平面幾何学に留まらず、球面幾何学にも拡張されます。球面上のサイクル四辺形においても、辺と対角線の関係は類似した形で表されます。この拡張は、特に天文学や航海術における球面三角法で利用され、球面上の角度や距離の計算に応用されています。
例えば、地球上の大規模な距離の計算や天体の位置を求める際に利用されます。
3.2 トレミーの不等式
トレミーの定理は、円に内接する四辺形に対してのみ成り立ちますが、内接していない四辺形に対しても、トレミーの不等式が適用されます。次の不等式が成り立ちます。
AC × BD ≥ AB × CD + AD × BC
円に内接する場合、等号が成立しますが、内接していない場合は等号が成立せず、対角線の積が辺の積の和より大きくなります。この不等式は、幾何学的な解析だけでなく、代数幾何や最適化の分野でも応用されています。
3.3 正多角形の解析
正多角形では、各頂点が円に内接しているため、トレミーの定理が適用されます。特に、正六角形や正八角形において、対角線と辺の比率を求める際に利用されます。
トレミーの定理は、円に内接する四辺形に対する幾何学的な関係を示す定理であり、サイクル四辺形や余弦定理と深く関連しています。また、球面幾何学やトレミーの不等式といった発展形があり、さまざまな問題に対して適用可能です。このため、トレミーの定理は、数学的な解析において強力なツールとなっています。
歴史的背景と影響

トレミーの定理が発見された時代背景
トレミーの定理は、紀元2世紀頃に活躍した古代ローマのギリシャ系天文学者・数学者、クラウディオス・プトレマイオス(Claudius Ptolemy)によって発見されました。彼の業績は、主に天文学や地理学におけるもので、特に天文学の基礎書『アルマゲスト』は非常に有名です。トレミーは、古代ギリシャの数学や天文学を集大成し、天文学における地球中心のモデルを提唱しましたが、数学の分野でもその理論は重要な役割を果たしました。
彼の定理が発表された時代、数学は主に天文学や測量、航海術と結びついて発展していました。天文学者たちは、天体の位置や動きを正確に予測するために、精密な三角法や幾何学的理論を必要としていました。その背景の中で、トレミーの定理は円や内接する四辺形の性質を利用して、天文学的な計算を支える重要な定理となりました。
トレミー以降の数学への影響や後世の数学者への貢献
トレミーの定理は、古代から中世、そして近代に至るまで数学や天文学の分野で大きな影響を与えました。後世のアラビアの数学者や天文学者たちは、ギリシャの知識を吸収し、発展させました。特に、アラビア世界ではギリシャの数学文献が翻訳され、広く学ばれたため、トレミーの業績はイスラム科学の基盤ともなりました。
例えば、9世紀に活躍したイスラム世界の天文学者で数学者のアル=バッターニ(Al-Battani)は、トレミーの天文学理論を洗練させ、より正確な計算方法を開発しました。また、11世紀にアラビア世界で活躍した数学者アブー・ライハーン・アル=ビールーニー(Al-Biruni)は、トレミーの幾何学理論を研究し、その成果を用いて地理的距離や天体の位置を正確に計算する技術を進化させました。
さらに、中世ヨーロッパでは、ルネサンス時代にトレミーの『アルマゲスト』がラテン語に翻訳され、再び注目を集めました。この時期には、ギリシャ数学やアラビア科学がヨーロッパの学問に再導入され、トレミーの定理も幾何学や三角法の発展に寄与しました。
古代ギリシャやアラビアの数学者との関係
トレミーの定理は、彼以前に活躍した古代ギリシャの数学者たちの理論に基づいています。特に、エウクレイデス(ユークリッド) や アルキメデス など、古代ギリシャの幾何学者たちが築いた数学的基礎が、トレミーの業績に大きな影響を与えました。彼らの研究があったからこそ、トレミーは円や四辺形に関する特性を探求し、独自の定理を発見することができました。
また、トレミーの定理が後にアラビア世界で広く研究され、アラビア数学の黄金期を支える知識の一つとなりました。この知識の蓄積は、後にヨーロッパに伝わり、近代数学や天文学の発展に大きく寄与しました。
まとめ
トレミーの定理の重要性とその普遍性
トレミーの定理は、古代から現代に至るまで、幾何学と天文学の両分野において非常に重要な役割を果たしてきました。特に、円に内接する四辺形の性質を明らかにすることにより、幾何学的問題の解決に役立つだけでなく、天文学や地理学、航海術における計算精度の向上にも貢献しました。
この定理の普遍性は、円に関連する多くの幾何学的問題や、現代の数学的解析にも適用できる点にあります。さらに、トレミーの定理は球面幾何学や三角法の基礎としても重要な位置を占めており、特に球面三角法において、天体の位置や地理的な距離を測るための理論的基盤を提供しています。
現代における定理の位置づけと学問的意義
現代においても、トレミーの定理は数学教育の一環として学ばれ、幾何学の基本定理の一つとして位置づけられています。特に、円に関する問題を扱う際には、この定理がしばしば登場します。さらに、現代の応用分野では、コンピュータービジョンや画像処理などの分野でも、この定理が幾何学的な基礎として利用されています。
また、トレミーの定理は、幾何学的な美しさや数学の普遍的な真理を示すものとして、数学者たちの間で今もなお評価されています。その数式が表す対称性や円に関する深い洞察は、数学者に限らず、理論物理学者やコンピューターサイエンティストたちにとっても貴重なツールとなっており、数学の理論的基盤として重要な役割を果たし続けています。
トレミーの定理は、古代から現代に至るまでの幾何学的問題の解決において欠かせない定理であり、その発展と応用は多岐にわたります。古代ギリシャやアラビアの数学者によって支えられたこの定理は、今日においても数学の基礎として、幅広い分野で活用され続けています。

